6. How to Solve ODEs with Rate Law Functions¶

6.1. ReactionRuleDescriptor¶

ReactionRule defines reactants, products, and a kinetic rate.

[2]:

rr1 = ReactionRule()
rr1.add_reactant(Species("A"))
rr1.add_reactant(Species("B"))
rr1.add_product(Species("C"))
rr1.set_k(1.0)
print(len(rr1.reactants()))  # => 2
print(len(rr1.products()))  # => 1
print(rr1.k())  # => 1.0
print(rr1.as_string())  # => A+B>C|1
print(rr1.has_descriptor())  # => False

2
1
1.0
A+B>C|1
False

In addition to that, ReactionRule could be extensible with ReactionRuleDescriptor.

[3]:

desc1 = ReactionRuleDescriptorMassAction(1.0)
print(desc1.k())
rr1.set_descriptor(desc1)

1.0

ReactionRuleDescriptor is accessible from ReactionRule.

[4]:

print(rr1.has_descriptor())
print(rr1.get_descriptor())
print(rr1.get_descriptor().k())

True
<ecell4_base.core.ReactionRuleDescriptorMassAction object at 0x147e2c4765e0>
1.0

ReactionRuleDescriptor can store stoichiometric coefficients for each reactants:

[5]:

desc1.set_reactant_coefficient(0, 2)  # Set a coefficient of the first reactant
desc1.set_reactant_coefficient(1, 3)  # Set a coefficient of the second reactant
desc1.set_product_coefficient(0, 4)  # Set a coefficient of the first product
print(rr1.as_string())

2*A+3*B>4*C|1

You can get the list of coefficients in the following way:

[6]:

print(desc1.reactant_coefficients())  # => [2.0, 3.0]
print(desc1.product_coefficients())  # => [4.0]

[2.0, 3.0]
[4.0]

Please be careful that ReactionRuleDescriptor works properly only with ode.

6.2. ReactionRuleDescriptorPyFunc¶

ReactionRuleDescriptor provides a function to calculate a derivative (flux or velocity) based on the given values of Species. In this section, we will explain the way to define your own kinetic law.

[7]:

rr1 = ReactionRule()
rr1.add_reactant(Species("A"))
rr1.add_reactant(Species("B"))
rr1.add_product(Species("C"))
print(rr1.as_string())

A+B>C|0

First, define a rate law function as a Python function. The function must accept six arguments and return a floating number. The first and second lists contain a value for each reactants and products respectively. The third and fourth represent volume and time. The coefficients of reactants and products are given in the last two arguments.

[8]:

def ratelaw(r, p, v, t, rc, pc):
    return 1.0 * r[0] * r[1] - 2.0 * p[0]

ReactionRuleDescriptorPyFunc accepts the function.

[9]:

desc1 = ReactionRuleDescriptorPyfunc(ratelaw, 'test')
desc1.set_reactant_coefficients([1, 1])
desc1.set_product_coefficients([1])
rr1.set_descriptor(desc1)
print(desc1.as_string())
print(rr1.as_string())

test
1*A+1*B>1*C|0

A lambda function is available too.

[10]:

desc2 = ReactionRuleDescriptorPyfunc(lambda r, p, v, t, rc, pc:  1.0 * r[0] * r[1] - 2.0 * p[0], 'test')
desc2.set_reactant_coefficients([1, 1])
desc2.set_product_coefficients([1])
rr1.set_descriptor(desc2)
print(desc1.as_string())
print(rr1.as_string())

test
1*A+1*B>1*C|0

To test if the function works properly, evaluate the value with ode.World.

[11]:

w = ode.World()
w.set_value(Species("A"), 10)
w.set_value(Species("B"), 20)
w.set_value(Species("C"), 30)

print(w.evaluate(rr1))  # => 140 = 1 * 10 * 20 - 2 * 30

140.0

6.3. NetworkModel¶

NetworkModel accepts ReactionRules with and without ReactionRuleDescriptor.

[12]:

m1 = NetworkModel()
rr1 = create_unbinding_reaction_rule(Species("C"), Species("A"), Species("B"), 3.0)
m1.add_reaction_rule(rr1)
rr2 = create_binding_reaction_rule(Species("A"), Species("B"), Species("C"), 0.0)
desc1 = ReactionRuleDescriptorPyfunc(lambda r, p, v, t, rc, pc: 0.1 * r[0] * r[1], "test")
desc1.set_reactant_coefficients([1, 1])
desc1.set_product_coefficients([1])
rr2.set_descriptor(desc1)
m1.add_reaction_rule(rr2)

You can access to the list of ReactionRules in NetworkModel via its member reaction_rules().

[13]:

print([rr.as_string() for rr in m1.reaction_rules()])

['C>A+B|3', '1*A+1*B>1*C|0']

Finally, you can run simulations in the same way with other solvers as follows:

[14]:

run_simulation(1.0, model=m1, y0={'A': 60, 'B': 60})

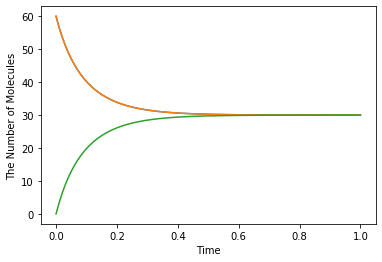
Modeling with Python decorators is also available by specifying a function instead of a rate (floating number). When a floating number is set, it is assumed to be a kinetic rate of a mass action reaction, but not a constant velocity.

[15]:

from functools import reduce
from operator import mul

with reaction_rules():
    A + B == C | (lambda r, *args: 0.1 * reduce(mul, r), 3.0)

m1 = get_model()

For the simplicity, you can directory defining the equation with Species names as follows:

[16]:

with reaction_rules():
    A + B == C | (0.1 * A * B, 3.0)

m1 = get_model()

When you call a Species (in the rate law) which is not listed as a reactant or product, it is automatically added to the list as an enzyme.

[17]:

with reaction_rules():
    S > P | 1.0 * E * S / (30.0 + S)

m1 = get_model()
print(m1.reaction_rules()[0].as_string())
print(m1.reaction_rules()[0].get_descriptor().as_string())

1*S+1*E>1*P+1*E|0
((1.0 * E * S) / (30.0 + S))

where E in the equation is appended to both reacant and product lists.

[18]:

run_simulation(10.0, model=m1, y0={'S': 60, 'E': 30})

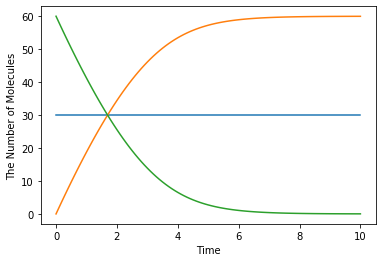
Please be careful about typo in Species’ name. When you make a typo, it is unintentionally recognized as a new enzyme:

[19]:

with reaction_rules():
    A13P2G > A23P2G | 1500 * A13B2G  # typo: A13P2G -> A13B2G

m1 = get_model()
print(m1.reaction_rules()[0].as_string())

1*A13P2G+1*A13B2G>1*A23P2G+1*A13B2G|0

When you want to disable the automatic declaration of enzymes, inactivate util.decorator.ENABLE_IMPLICIT_DECLARATION. If its value is False, the above case will raise an error:

[20]:

import ecell4.util.decorator
ecell4.util.decorator.ENABLE_IMPLICIT_DECLARATION = False

try:
    with reaction_rules():
        A13P2G > A23P2G | 1500 * A13B2G
except RuntimeError as e:
    print(repr(e))

ecell4.util.decorator.ENABLE_IMPLICIT_DECLARATION = True

RuntimeError('[A13B2G] is unknown [(1500 * {0})].')

Although E-Cell4 is specialized for a simulation of biochemical reaction network, by using a synthetic reaction rule, ordinary differential equations can be translated intuitively. For example, the Lotka-Volterra equations:

where \(A=1.5, B=1, C=3, D=1, x(0)=10, y(0)=5\), are solved as follows:

[21]:

with reaction_rules():
    A, B, C, D = 1.5, 1, 3, 1

    ~x > x | A * x - B * x * y
    ~y > y | -C * y + D * x * y

run_simulation(10, model=get_model(), y0={'x': 10, 'y': 5})

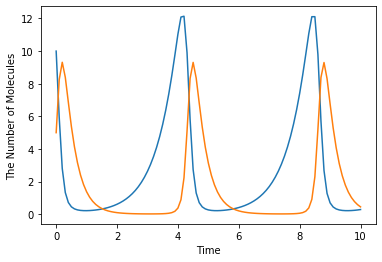
6.4. References in a Rate Law¶

Here, we exlain the details in the rate law definition.

First, when you use simpler definitions of a rate law with Species, only a limited number of mathematical functions (e.g. exp, log, sin, cos, tan, asin, acos, atan, and pi) are available there even if you declare the function outside the block.

[22]:

try:
    from math import erf

    with reaction_rules():
        S > P | erf(S / 30.0)
except TypeError as e:
    print(repr(e))

TypeError('must be real number, not DivExp')

This error happens because erf is tried to be evaluated agaist S / 30.0, which is not a floating number. In contrast, the following case is acceptable:

[23]:

from math import erf

with reaction_rules():
    S > P | erf(2.0) * S

m1 = get_model()
print(m1.reaction_rules()[0].get_descriptor().as_string())

(0.9953222650189527 * S)

where only the result of erf(2.0), 0.995322265019, is passed to the rate law. Thus, the rate law above has no reference to the erf function. Similarly, a value of variables declared outside is acceptable, but not as a reference.

[24]:

kcat, Km = 1.0, 30.0

with reaction_rules():
    S > P | kcat * E * S / (Km + S)

m1 = get_model()
print(m1.reaction_rules()[0].get_descriptor().as_string())
kcat = 2.0  # This doesn't affect the model
print(m1.reaction_rules()[0].get_descriptor().as_string())

((1.0 * E * S) / (30.0 + S))
((1.0 * E * S) / (30.0 + S))

Even if you change the value of a variable, it does not affect the rate law.

On the other hand, when you use your own function to define a rate law, it can hold a reference to variables outside.

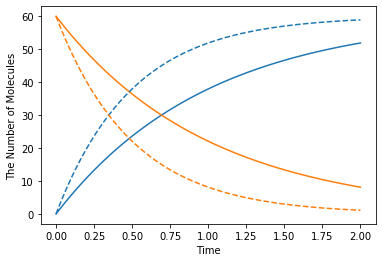
[25]:

k1 = 1.0

with reaction_rules():
    S > P | (lambda r, *args: k1 * r[0])  # referring k1

m1 = get_model()

ret1 = run_simulation(2, model=m1, y0={"S": 60})
k1 = 2.0  # This could change the result
ret2 = run_simulation(2, model=m1, y0={"S": 60})

plotting.plot_number_observer(ret1, '-', ret2, '--')

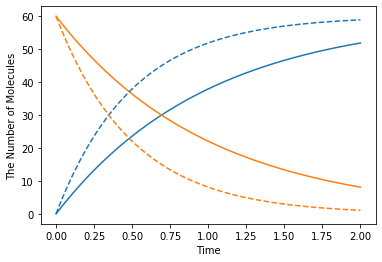
However, in this case, it is better to make a new model for each set of parameters.

[26]:

def create_model(k):
    with reaction_rules():
        S > P | k

    return get_model()

ret1 = run_simulation(2, model=create_model(k=1.0), y0={"S": 60})
ret2 = run_simulation(2, model=create_model(k=2.0), y0={"S": 60})
plotting.plot_number_observer(ret1, '-', ret2, '--')

6.5. More about ODEs¶

In ode.World, a value for each Species is a floating number. However, for the compatibility, the common member num_molecules and add_molecules regard the value as an integer.

[27]:

w = ode.World()
w.add_molecules(Species("A"), 2.5)
print(w.num_molecules(Species("A")))

2

To set/get a real number, use set_value and get_value:

[28]:

w.set_value(Species("B"), 2.5)
print(w.get_value(Species("A")))
print(w.get_value(Species("B")))

2.5
2.5

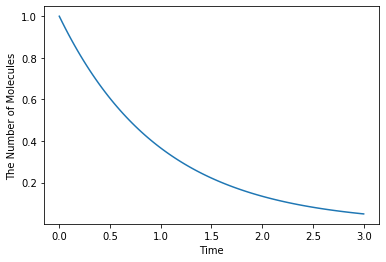
As a default, ode.Simulator employs the Rosenblock method, called ROSENBROCK4_CONTROLLER, to solve ODEs. In addition to that, two solvers, EULER and RUNGE_KUTTA_CASH_KARP54, are available. ROSENBROCK4_CONTROLLER and RUNGE_KUTTA_CASH_KARP54 adaptively change the step size during time evolution due to error controll, but EULER does not.

[29]:

with reaction_rules():
    A > ~A | 1.0

m1 = get_model()

w1 = ode.World()
w1.set_value(Species("A"), 1.0)
sim1 = ode.Simulator(w1, m1, ode.EULER)
sim1.set_dt(0.01) # This is only effective for EULER
obs1 = FixedIntervalNumberObserver(0.1)
sim1.run(3.0, obs1)

ode.Factory also accepts a solver type and a default step interval.

[30]:

run_simulation(3.0, model=m1, y0={"A": 1.0}, solver=('ode', ode.EULER, 0.01))

See also the examples listed below:

• Glycolysis of Human Erythrocytes

• Drosophila Circadian Clock

• Attractors