See also
This page was generated from examples/example07.ipynb.
Download the Jupyter Notebook for this section: example07.ipynb. View in nbviewer.
Lotka-Volterra 2D¶
[1]:
%matplotlib inline
from ecell4.prelude import *
The Original Model in Ordinary Differential Equations¶
[2]:
alpha = 1
with reaction_rules():
~u > u | u * (1 - v)
~v > v | alpha * v * (u - 1)
m = get_model()
[3]:
run_simulation(15, {'u': 1.25, 'v': 0.66}, model=m).plot(legend=True)
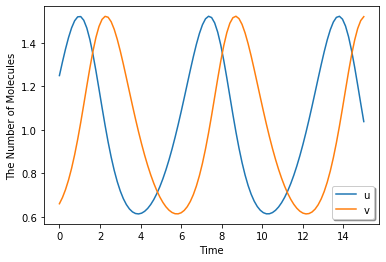
The Modified Model Decomposed into Elementary Reactions¶
[4]:
alpha = 1
with species_attributes():
u | {'D': 0.1}
v | {'D': 0.1}
with reaction_rules():
u > u + u | 1.0
u + v > v | 1.0
u + v > u + v2 | alpha
v2 > v + v | alpha * 10000.0
v > ~v | alpha
m = get_model()
[5]:
session = Session(model=m, y0={'u': 1.25 * 1600, 'v': 0.66 * 1600}, volume=1600)
[6]:
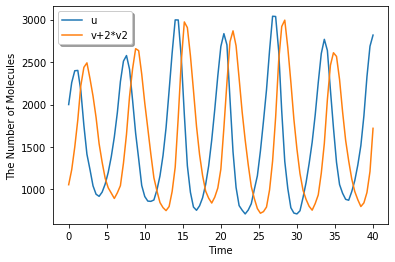
session.run(40).plot(y=['u', 'v+2*v2'], legend=True)
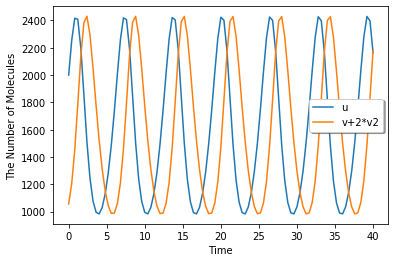
[7]:
session.run(40, ndiv=100, solver='gillespie').plot(y=['u', 'v+2*v2'], legend=True)
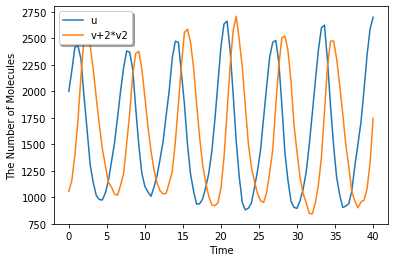
[8]:
alpha = 1
with species_attributes():
u | v | {'D': 0.1}
with reaction_rules():
u > u + u | 1.0
u + v > v | 1.0
u + v > u + v + v | alpha
v > ~v | alpha
m = get_model()
[9]:
session = Session(model=m, y0={'u': 1.25 * 1600, 'v': 0.66 * 1600}, volume=1600)
[10]:
session.run(40).plot(y=['u', 'v+2*v2'], legend=True)
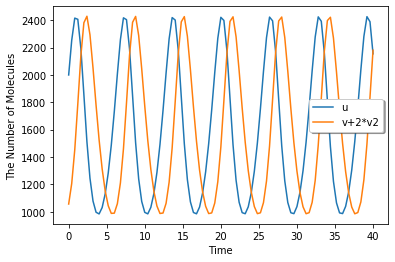
[11]:
session.run(40, ndiv=100, solver='gillespie').plot(y=['u', 'v+2*v2'], legend=True)
A Lotka-Volterra-like Model in 2D¶
[12]:
V = 1600.0
session = Session(model=m, y0={'u': 1.25 * V, 'v': 0.66 * V}, volume=Real3(40, 40, 1))
[13]:
ret = session.run(
100, ndiv=1000, solver=('meso', Integer3(160, 160, 1)), rndseed=0,
observers=FixedIntervalHDF5Observer(2, "test%03d.h5"))
[14]:
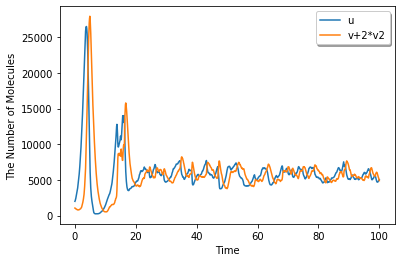
ret.plot(y=['u', 'v+2*v2'], legend=True)
[15]:
assert V == ret.world.volume()
[16]:
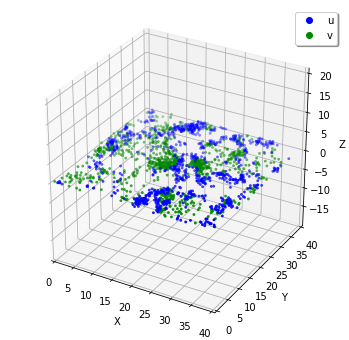
show(ret.world)
[17]:
plotting.plot_movie_with_attractive_mpl(
ret.observers[1], linewidth=0, noaxis=True, figsize=6, whratio=1.4,
angle=(-90, 90, 6), bitrate='10M')