See also
This page was generated from examples/example13.ipynb.
Download the Jupyter Notebook for this section: example13.ipynb. View in nbviewer.
Multiary Complex Model of GPCR Signaling Activations¶
This notebook is the Supplemental Material for ``Watabe et al. Multiary complex formations in GPCR signaling activations. arXiv:xxx.xxxxxx (2020)”.
[1]:
# Multiary Complex Model in GPCR signaling activation
import os
import sys
import numpy
%matplotlib inline
import matplotlib.pylab as plt
from ecell4.prelude import *
Parameters¶
[2]:
class ParConfigs() :
'''
Set Parameters
'''
# Set model parameters
def __init__(self, user_configs_dict = None):
self.A = 10000. # Cell-Area: µm^2
self.T = 4.977 # Receptor concetration: receptors/µm^2
self.r0 = int(self.T*self.A)
# ligand-receptor first-order interactions
# Phi <==> M
# Phi' <==> M'
# M' <==> D'
# dissociation rates
self.dl0 = 1.00 # 1/sec
self.dl1 = 1.00 # 1/sec
self.dl2 = 1.00 # 1/sec
# equilibrium constants
self.Kl0 = 1.00 # nM
self.Kl1 = None
self.Kl2 = None
# receptor-Gprotein first-order interactions
# Phi <==> G Phi
# Phi' <==> G Phi'
# dissociation rates
self.dg0 = 1.00 # 1/sec
self.dg1 = 1.00 # 1/sec
# equilibrium constants
self.Kg0 = 1.00 # nM
self.Kg1 = None
# ligand-(receptor-Gprotein) first-order interactions
# G Phi <==> G M
# G Phi' <==> G M'
# G M' <==> G D'
# dissociation rates
self.da0 = 1.00 # 1/sec
self.da1 = 1.00 # 1/sec
self.da2 = 1.00 # 1/sec
# equilibrium constants
self.Ka0 = 1.00 # nM
self.Ka1 = None
self.Ka2 = None
# Gprotein-(ligand-receptor) first-order interactions
# M <==> G M
# M' <==> G M'
# D' <==> G D'
# dissociation rates
self.db0 = 1.00 # 1/sec
self.db1 = 1.00 # 1/sec
self.db2 = 1.00 # 1/sec
# equilibrium constants
self.Kb0 = 1.00 # nM
self.Kb1 = None
self.Kb2 = None
# receptor-receptor interactions:
# Phi + Phi <==> Phi'
# M + Phi <==> M'
# M + M <==> D'
# dissociation rates
self.dx0 = 1.00 # 1/sec
self.dx1 = 1.00 # 1/sec
self.dx2 = 1.00 # 1/sec
# equilibrium constants
self.Kx0 = None
self.Kx1 = None
self.Kx2 = None
# receptor-Gprotein coupling
# G Phi + Phi <==> G Phi'
# G M + Phi <==> G M'
# G Phi + M <==> G M'
# G M + M <==> G D'
# dissociation rates
self.dy0 = 1.00 # 1/sec
self.dy1 = 1.00 # 1/sec
self.dy2 = 1.00 # 1/sec
self.dy3 = 1.00 # 1/sec
# equilibrium constants
self.Ky0 = None
self.Ky1 = None
self.Ky2 = None
self.Ky3 = None
def get_r0(self):
r0 = self.r0
return r0
def get_dl(self):
dl0 = self.dl0
dl1 = self.dl1
dl2 = self.dl2
return dl0, dl1, dl2
def get_kl(self, sigma_l1, sigma_l2):
self.Kl1 = sigma_l1*self.Kl0
self.Kl2 = sigma_l2*self.Kl0
kl0 = self.dl0/self.Kl0 # 1/(sec nM)
kl1 = self.dl1/self.Kl1 # 1/(sec nM)
kl2 = self.dl2/self.Kl2 # 1/(sec nM)
return kl0, kl1, kl2
def get_dg(self):
dg0 = self.dg0
dg1 = self.dg1
return dg0, dg1
def get_kg(self, sigma_g1):
self.Kg1 = sigma_g1*self.Kg0
kg0 = self.dg0/self.Kg0
kg1 = self.dg1/self.Kg1
return kg0, kg1
def get_da(self):
da0 = self.da0
da1 = self.da1
da2 = self.da2
return da0, da1, da2
def get_ka(self, alpha, sigma_a1, sigma_a2):
self.Ka0 = alpha*self.Kl0
self.Ka1 = sigma_a1*self.Ka0
self.Ka2 = sigma_a2*self.Ka0
ka0 = self.da0/self.Ka0
ka1 = self.da1/self.Ka1
ka2 = self.da2/self.Ka2
return ka0, ka1, ka2
def get_db(self):
db0 = self.db0
db1 = self.db1
db2 = self.db2
return db0, db1, db2
def get_kb(self, beta, sigma_b1, sigma_b2):
self.Kb0 = beta*self.Kg0
self.Kb1 = sigma_b1*self.Kb0
self.Kb2 = sigma_b2*self.Kb0
kb0 = self.db0/self.Kb0
kb1 = self.db1/self.Kb1
kb2 = self.db2/self.Kb2
return kb0, kb1, kb2
def get_dx(self):
dx0 = self.dx0
dx1 = self.dx1
dx2 = self.dx2
return dx0, dx1, dx2
def get_kx(self, kx, N):
self.Kx0 = self.T/kx # 1/µm^2
self.Kx1 = (self.Kl1*self.Kx0)/self.Kl0 # 1/µm^2
self.Kx2 = (self.Kl2*self.Kl1*self.Kx0)/(self.Kl0**2) # 1/µm^2
kx0 = self.dx0/self.Kx0 # µm^2/sec
kx1 = self.dx1/self.Kx1 # µm^2/sec
kx2 = self.dx2/self.Kx2 # µm^2/sec
return kx0/N, kx1/N, kx2/N
def get_dy(self):
dy0 = self.dy0
dy1 = self.dy1
dy2 = self.dy2
dy3 = self.dy3
return dy0, dy1, dy2, dy3
def get_ky(self, sigma_y0, sigma_y1, sigma_y2, sigma_y3):
self.Ky0 = sigma_y0*self.Kx0
self.Ky1 = sigma_y1*self.Kx1
self.Ky2 = sigma_y2*self.Kx1
self.Ky3 = sigma_y3*self.Kx2
ky0 = self.dy0/self.Ky0 # µm^2/sec
ky1 = self.dy1/self.Ky1 # µm^2/sec
ky2 = self.dy2/self.Ky2 # µm^2/sec
ky3 = self.dy3/self.Ky3 # µm^2/sec
return ky0, ky1, ky2, ky3
[3]:
def run_N0(m, mols, obs0):
# Create simulator (ODE)
w = ode.World()
w.bind_to(m)
sim = ode.Simulator(w)
# Initialization
print ("Initial condition")
for i in range(len(mols)) :
obs0_i = int(round(obs0[i]))
w.add_molecules(Species("%s" % (mols[i])), obs0_i)
print (mols[i], ':', obs0_i)
sim.initialize()
# Run simulator
period = 50. # sec
obs = FixedIntervalNumberObserver(1.0, mols)
sim.run(period, [obs])
obs_data = numpy.array(obs.data())
time = obs_data[:,0]
R0 = obs_data[:,1]
RM = numpy.zeros(shape=(len(time)))
RD = obs_data[:,2]
G0 = obs_data[:,3]
GM = obs_data[:,4]
GD = numpy.zeros(shape=(len(time)))
data = obs_data.T
plt.plot(data[0], RM+RD+GM+GD, "b-", label="Bound states")
plt.plot(data[0], RM, "-", label="M")
plt.plot(data[0], RD, "-", label="D")
plt.plot(data[0], GM, "-", label="G•M")
plt.plot(data[0], GM, "-", label="G•D")
plt.xlabel("Time [sec]")
plt.ylabel("Bounds")
plt.xlim(data[0][0], data[0][-1])
plt.legend(loc="best", shadow=True)
plt.show()
[4]:
def run_N1(m, mols, obs0):
# Create simulator (ODE)
w = ode.World()
w.bind_to(m)
sim = ode.Simulator(w)
# Initialization
print ("Initial condition")
for i in range(len(mols)) :
obs0_i = int(round(obs0[i]))
w.add_molecules(Species("%s" % (mols[i])), obs0_i)
print (mols[i], ':', obs0_i)
sim.initialize()
# Run simulator
period = 50. # sec
obs = FixedIntervalNumberObserver(1.0, mols)
sim.run(period, [obs])
obs_data = numpy.array(obs.data())
time = obs_data[:,0]
R0 = obs_data[:,1] + obs_data[:,2]
RM = obs_data[:,3] + obs_data[:,4]
RD = obs_data[:,5]
G0 = obs_data[:,6] + obs_data[:,7]
GM = obs_data[:,8] + obs_data[:,9]
GD = obs_data[:,10]
data = obs_data.T
plt.plot(data[0], RM+RD+GM+GD, "b-", label="Bound states")
plt.plot(data[0], RM, "-", label="M")
plt.plot(data[0], RD, "-", label="D")
plt.plot(data[0], GM, "-", label="G•M")
plt.plot(data[0], GM, "-", label="G•D")
plt.xlabel("Time [sec]")
plt.ylabel("Bounds")
plt.xlim(data[0][0], data[0][-1])
plt.legend(loc="best", shadow=True)
plt.show()
[5]:
def run_N2(m, mols, obs0):
# Create simulator (ODE)
w = ode.World()
w.bind_to(m)
sim = ode.Simulator(w)
# Initialization
print ("Initial condition")
for i in range(len(mols)) :
obs0_i = int(round(obs0[i]))
w.add_molecules(Species("%s" % (mols[i])), obs0_i)
print (mols[i], ':', obs0_i)
sim.initialize()
# Run simulator
period = 50. # sec
obs = FixedIntervalNumberObserver(1.0, mols)
sim.run(period, [obs])
obs_data = numpy.array(obs.data())
time = obs_data[:,0]
R0 = obs_data[:,1] + obs_data[:,2] + obs_data[:,3] + obs_data[:,4]
RM = obs_data[:,5] + obs_data[:,6] + obs_data[:,7] + obs_data[:,8]
RD = obs_data[:,9] + obs_data[:,10] + obs_data[:,11]
G0 = obs_data[:,12] + obs_data[:,13] + obs_data[:,14] + obs_data[:,15]
GM = obs_data[:,16] + obs_data[:,17] + obs_data[:,18] + obs_data[:,19]
GD = obs_data[:,20] + obs_data[:,21] + obs_data[:,22]
data = obs_data.T
plt.plot(data[0], RM+RD+GM+GD, "b-", label="Bound states")
plt.plot(data[0], RM, "-", label="M")
plt.plot(data[0], RD, "-", label="D")
plt.plot(data[0], GM, "-", label="G•M")
plt.plot(data[0], GM, "-", label="G•D")
plt.xlabel("Time [sec]")
plt.ylabel("Bounds")
plt.xlim(data[0][0], data[0][-1])
plt.legend(loc="best", shadow=True)
plt.show()
[6]:
def run_N3(m, mols, obs0):
# Create simulator (ODE)
w = ode.World()
w.bind_to(m)
sim = ode.Simulator(w)
# Initialization
print ("Initial condition")
for i in range(len(mols)) :
obs0_i = int(round(obs0[i]))
w.add_molecules(Species("%s" % (mols[i])), obs0_i)
print (mols[i], ':', obs0_i)
sim.initialize()
# Run simulator
period = 50. # sec
obs = FixedIntervalNumberObserver(1.0, mols)
sim.run(period, [obs])
obs_data = numpy.array(obs.data())
time = obs_data[:,0]
R0 = obs_data[:,1] + obs_data[:,2] + obs_data[:,3] + obs_data[:,4] + obs_data[:,5] + obs_data[:,6]
RM = obs_data[:,7] + obs_data[:,8] + obs_data[:,9] + obs_data[:,10] + obs_data[:,11] + obs_data[:,12]
RD = obs_data[:,13] + obs_data[:,14] + obs_data[:,15] + obs_data[:,16] + obs_data[:,17]
G0 = obs_data[:,18] + obs_data[:,19] + obs_data[:,20] + obs_data[:,21] + obs_data[:,22] + obs_data[:,23]
GM = obs_data[:,24] + obs_data[:,25] + obs_data[:,26] + obs_data[:,27] + obs_data[:,28] + obs_data[:,29]
GD = obs_data[:,30] + obs_data[:,31] + obs_data[:,32] + obs_data[:,33] + obs_data[:,34]
data = obs_data.T
plt.plot(data[0], RM+RD+GM+GD, "b-", label="Bound states")
plt.plot(data[0], RM, "-", label="M")
plt.plot(data[0], RD, "-", label="D")
plt.plot(data[0], GM, "-", label="G•M")
plt.plot(data[0], GM, "-", label="G•D")
plt.xlabel("Time [sec]")
plt.ylabel("Bounds")
plt.xlim(data[0][0], data[0][-1])
plt.legend(loc="best", shadow=True)
plt.show()
[7]:
def run_N4(m, mols, obs0):
# Create simulator (ODE)
w = ode.World()
w.bind_to(m)
sim = ode.Simulator(w)
# Initialization
print ("Initial condition")
for i in range(len(mols)) :
obs0_i = int(round(obs0[i]))
w.add_molecules(Species("%s" % (mols[i])), obs0_i)
print (mols[i], ':', obs0_i)
sim.initialize()
# Run simulator
period = 50. # sec
obs = FixedIntervalNumberObserver(1.0, mols)
sim.run(period, [obs])
obs_data = numpy.array(obs.data())
time = obs_data[:,0]
R0 = obs_data[:,1] + obs_data[:,2] + obs_data[:,3] + obs_data[:,4] + obs_data[:,5] + obs_data[:,6] + obs_data[:,7] + obs_data[:,8]
RM = obs_data[:,9] + obs_data[:,10] + obs_data[:,11] + obs_data[:,12] + obs_data[:,13] + obs_data[:,14] + obs_data[:,15] + obs_data[:,16]
RD = obs_data[:,17] + obs_data[:,18] + obs_data[:,19] + obs_data[:,20] + obs_data[:,21] + obs_data[:,22] + obs_data[:,23]
G0 = obs_data[:,24] + obs_data[:,25] + obs_data[:,26] + obs_data[:,27] + obs_data[:,28] + obs_data[:,29] + obs_data[:,30] + obs_data[:,31]
GM = obs_data[:,32] + obs_data[:,33] + obs_data[:,34] + obs_data[:,35] + obs_data[:,36] + obs_data[:,37] + obs_data[:,38] + obs_data[:,39]
GD = obs_data[:,40] + obs_data[:,41] + obs_data[:,42] + obs_data[:,43] + obs_data[:,44] + obs_data[:,45] + obs_data[:,46]
data = obs_data.T
plt.plot(data[0], RM+RD+GM+GD, "b-", label="Bound states")
plt.plot(data[0], RM, "-", label="M")
plt.plot(data[0], RD, "-", label="D")
plt.plot(data[0], GM, "-", label="G•M")
plt.plot(data[0], GM, "-", label="G•D")
plt.xlabel("Time [sec]")
plt.ylabel("Bounds")
plt.xlim(data[0][0], data[0][-1])
plt.legend(loc="best", shadow=True)
plt.show()
[8]:
def run_N5(m, mols, obs0):
# Create simulator (ODE)
w = ode.World()
w.bind_to(m)
sim = ode.Simulator(w)
# Initialization
print ("Initial condition")
for i in range(len(mols)) :
obs0_i = int(round(obs0[i]))
w.add_molecules(Species("%s" % (mols[i])), obs0_i)
print (mols[i], ':', obs0_i)
sim.initialize()
# Run simulator
period = 50. # sec
obs = FixedIntervalNumberObserver(1.0, mols)
sim.run(period, [obs])
obs_data = numpy.array(obs.data())
time = obs_data[:,0]
R0 = obs_data[:,1] + obs_data[:,2] + obs_data[:,3] + obs_data[:,4] + obs_data[:,5] + obs_data[:,6] + obs_data[:,7] + obs_data[:,8] + obs_data[:,9] + obs_data[:,10]
RM = obs_data[:,11] + obs_data[:,12] + obs_data[:,13] + obs_data[:,14] + obs_data[:,15] + obs_data[:,16] + obs_data[:,17] + obs_data[:,18] + obs_data[:,19] + obs_data[:,20]
RD = obs_data[:,21] + obs_data[:,22] + obs_data[:,23] + obs_data[:,24] + obs_data[:,25] + obs_data[:,26] + obs_data[:,27] + obs_data[:,28] + obs_data[:,29]
G0 = obs_data[:,30] + obs_data[:,31] + obs_data[:,32] + obs_data[:,33] + obs_data[:,34] + obs_data[:,35] + obs_data[:,36] + obs_data[:,37] + obs_data[:,38] + obs_data[:,39]
GM = obs_data[:,40] + obs_data[:,41] + obs_data[:,42] + obs_data[:,43] + obs_data[:,44] + obs_data[:,45] + obs_data[:,46] + obs_data[:,47] + obs_data[:,48] + obs_data[:,49]
GD = obs_data[:,50] + obs_data[:,51] + obs_data[:,52] + obs_data[:,53] + obs_data[:,54] + obs_data[:,55] + obs_data[:,56] + obs_data[:,57] + obs_data[:,58]
data = obs_data.T
plt.plot(data[0], RM+RD+GM+GD, "b-", label="Bound states")
plt.plot(data[0], RM, "-", label="M")
plt.plot(data[0], RD, "-", label="D")
plt.plot(data[0], GM, "-", label="G•M")
plt.plot(data[0], GM, "-", label="G•D")
plt.xlabel("Time [sec]")
plt.ylabel("Bounds")
plt.xlim(data[0][0], data[0][-1])
plt.legend(loc="best", shadow=True)
plt.show()
The simplest ternary complex model (kx = 0)¶
[9]:
# this is the ternary complex model (TCM): N=0
N = 0.00
# Inputs :
# Ligand and G-protein concentrations
L = 1.00
G = 1.00
# scaling factor
alpha = 1.00
# The lumped dimensionless parameter
kx = 0.00
mols = ["r", "R", "Gr", "GR"]
par = ParConfigs()
obs0 = numpy.zeros(shape=(len(mols)))
obs0[0] = par.get_r0()
###############################################################
print ('Model-order: N =', N)
print ('Ligand: L =', L)
print ('G-protein: G =', G)
print ('alpha-factor: a =', alpha)
print ('Initial condition:')
for i in range(len(mols)) :
print (' ', mols[i], ': ', obs0[i])
###############################################################
# ligands-receptors first-order coupling
dl0, dl1, dl2 = par.get_dl()
kl0, kl1, kl2 = par.get_kl(100, 100)
# Gproteins-receptors first-order coupling
dg0, dg1 = par.get_dg()
kg0, kg1 = par.get_kg(100)
# ligand-(Gproteins-receptors) first-order coupling
da0, da1, da2 = par.get_da()
ka0, ka1, ka2 = par.get_ka(alpha, 100, 100)
# Gproteins-(ligand-receptors) first-order coupling
db0, db1, db2 = par.get_db()
kb0, kb1, kb2 = par.get_kb(alpha, 100, 100)
## receptor-receptor second-order coupling
#dx0, dx1, dx2 = par.get_dx()
#kx0, kx1, kx2 = par.get_kx(kx, N)
#
## receptor-Gprotein second-order coupling
#dy0, dy1, dy2, dy3 = par.get_dy()
#ky0, ky1, ky2, ky3 = par.get_ky(1, 1, 1, 1)
Model-order: N = 0.0
Ligand: L = 1.0
G-protein: G = 1.0
alpha-factor: a = 1.0
Initial condition:
r : 49770.0
R : 0.0
Gr : 0.0
GR : 0.0
[10]:
with reaction_rules():
# TCM (Ternary complex model)
r == R | (kl0*L, dl0)
R == GR | (ka0*G, da0)
r == Gr | (kg0*G, dg0)
Gr == GR | (kb0*L, db0)
m = get_model()
show(m)
r > R | 1.0
R > r | 1.0
R > GR | 1.0
GR > R | 1.0
r > Gr | 1.0
Gr > r | 1.0
Gr > GR | 1.0
GR > Gr | 1.0
[11]:
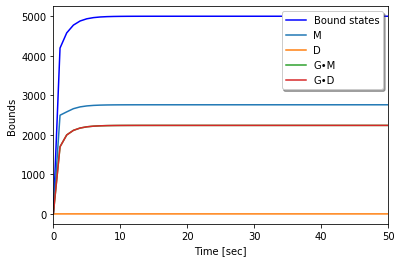
run_N0(m, mols, obs0)
Initial condition
r : 49770
R : 0
Gr : 0
GR : 0
The multiary complex model¶
Monovalent model (N = 1 and kx > 0)¶
[12]:
# this is the monovalent model : N=1
N = 1.00
# Inputs :
# Ligand and G-protein concentrations
L = 1.00
G = 1.00
# scaling factor
alpha = 1.00
# The lumped dimensionless parameter (kx > 0)
kx = 0.001
# get model-parameters
par = ParConfigs()
mols = ["r", "rr", "R", "rR", "RR", "Gr", "Grr", "GR", "GrR", "GRR"]
obs0 = numpy.zeros(shape=(len(mols)))
obs0[0] = par.get_r0()
###############################################################
print ('Model-order: N =', N)
print ('Ligand: L =', L)
print ('G-protein: G =', G)
print ('alpha-factor: a =', alpha)
print ('Initial condition:')
for i in range(len(mols)) :
print (' ', mols[i], ': ', obs0[i])
###############################################################
# ligands-receptors first-order coupling
dl0, dl1, dl2 = par.get_dl()
kl0, kl1, kl2 = par.get_kl(100, 100)
# Gproteins-receptors first-order coupling
dg0, dg1 = par.get_dg()
kg0, kg1 = par.get_kg(100)
# ligand-(Gproteins-receptors) first-order coupling
da0, da1, da2 = par.get_da()
ka0, ka1, ka2 = par.get_ka(alpha, 100, 100)
# Gproteins-(ligand-receptors) first-order coupling
db0, db1, db2 = par.get_db()
kb0, kb1, kb2 = par.get_kb(alpha, 100, 100)
# receptor-receptor second-order coupling
dx0, dx1, dx2 = par.get_dx()
kx0, kx1, kx2 = par.get_kx(kx, N)
# receptor-Gprotein second-order coupling
dy0, dy1, dy2, dy3 = par.get_dy()
ky0, ky1, ky2, ky3 = par.get_ky(1, 1, 1, 1)
Model-order: N = 1.0
Ligand: L = 1.0
G-protein: G = 1.0
alpha-factor: a = 1.0
Initial condition:
r : 49770.0
rr : 0.0
R : 0.0
rR : 0.0
RR : 0.0
Gr : 0.0
Grr : 0.0
GR : 0.0
GrR : 0.0
GRR : 0.0
[13]:
with reaction_rules():
# TCM (Ternary complex model)
r == R | (kl0*L, dl0)
R == GR | (ka0*G, da0)
r == Gr | (kg0*G, dg0)
Gr == GR | (kb0*L, db0)
# receptor dimerization
r + r == rr | (kx0, dx0)
R + r == rR | (kx1, dx1)
R + R == RR | (kx2, dx2)
rr == rR | (kl1*L, dl1)
rR == RR | (kl2*L, dl2)
# dimers coupled with G-proteins
rr == Grr | (kg1*G, dg1)
rR == GrR | (kb1*G, db1)
RR == GRR | (kb2*G, db2)
Gr + r == Grr | (ky0, dy0)
GR + r == GrR | (ky1, dy1)
Gr + R == GrR | (ky2, dy2)
GR + R == GrR | (ky3, dy3)
Grr == GrR | (ka1*L, da1)
GrR == GRR | (ka2*L, da2)
m = get_model()
show(m)
r > R | 1.0
R > r | 1.0
R > GR | 1.0
GR > R | 1.0
r > Gr | 1.0
Gr > r | 1.0
Gr > GR | 1.0
GR > Gr | 1.0
r + r > rr | 0.00020092425155716296
rr > r + r | 1.0
R + r > rR | 2.0092425155716294e-06
rR > R + r | 1.0
R + R > RR | 2.0092425155716296e-08
RR > R + R | 1.0
rr > rR | 0.01
rR > rr | 1.0
rR > RR | 0.01
RR > rR | 1.0
rr > Grr | 0.01
Grr > rr | 1.0
rR > GrR | 0.01
GrR > rR | 1.0
RR > GRR | 0.01
GRR > RR | 1.0
Gr + r > Grr | 0.00020092425155716296
Grr > Gr + r | 1.0
GR + r > GrR | 2.0092425155716294e-06
GrR > GR + r | 1.0
Gr + R > GrR | 2.0092425155716294e-06
GrR > Gr + R | 1.0
GR + R > GrR | 2.0092425155716296e-08
GrR > GR + R | 1.0
Grr > GrR | 0.01
GrR > Grr | 1.0
GrR > GRR | 0.01
GRR > GrR | 1.0
[14]:
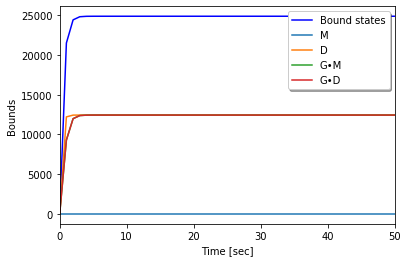
run_N1(m, mols, obs0)
Initial condition
r : 49770
rr : 0
R : 0
rR : 0
RR : 0
Gr : 0
Grr : 0
GR : 0
GrR : 0
GRR : 0
Bivalent model (N = 2 and kx > 0)¶
[15]:
# this is the bivalent model : N=2
N = 2.00
mols = ["r", "rr", "rrr", "rrrr",
"R", "rR", "rrR", "rrrR",
"RR", "rRR", "rrRR",
"Gr", "Grr", "Grrr", "Grrrr",
"GR", "GrR", "GrrR", "GrrrR",
"GRR", "GrRR", "GrrRR"]
[16]:
with reaction_rules():
# TCM (Ternary complex model)
r == R | (kl0*L, dl0)
R == GR | (ka0*G, da0)
r == Gr | (kg0*G, dg0)
Gr == GR | (kb0*L, db0)
# receptor dimerization
r + r == rr | (kx0, dx0)
r + rr == rrr | (kx0, dx0)
rr + r == rrr | (kx0, dx0)
rr + rr == rrrr | (kx0, dx0)
R + r == rR | (kx1, dx1)
R + rr == rrR | (kx1, dx1)
rR + r == rrR | (kx1, dx1)
rR + rr == rrrR | (kx1, dx1)
R + R == RR | (kx2, dx2)
R + rR == rRR | (kx2, dx2)
rR + R == rRR | (kx2, dx2)
rR + rR == rrRR | (kx2, dx2)
rr == rR | (kl1*L, dl1)
rrr == rrR | (kl1*L, dl1)
rrrr == rrrR | (kl1*L, dl1)
rR == RR | (kl2*L, dl2)
rrR == rRR | (kl2*L, dl2)
rrrR == rrRR | (kl2*L, dl2)
# dimers coupled with G-proteins
rr == Grr | (kg1*G, dg1)
rrr == Grrr | (kg1*G, dg1)
rrrr == Grrrr | (kg1*G, dg1)
rR == GrR | (kb1*G, db1)
rrR == GrrR | (kb1*G, db1)
rrrR == GrrrR | (kb1*G, db1)
RR == GRR | (kb2*G, db2)
rRR == GrRR | (kb2*G, db2)
rrRR == GrrRR | (kb2*G, db2)
Gr + r == Grr | (ky0, dy0)
Gr + rr == Grrr | (ky0, dy0)
Grr + r == Grrr | (ky0, dy0)
Grr + rr == Grrrr | (ky0, dy0)
GR + r == GrR | (ky1, dy1)
GR + rr == GrrR | (ky1, dy1)
GrR + r == GrrR | (ky1, dy1)
GrR + rr == GrrrR | (ky1, dy1)
R + Gr == GrR | (ky2, dy2)
R + Grr == GrrR | (ky2, dy2)
rR + Gr == GrrR | (ky2, dy2)
rR + Grr == GrrrR | (ky2, dy2)
GR + R == GRR | (ky3, dy3)
GR + rR == GrRR | (ky3, dy3)
GrR + R == GrRR | (ky3, dy3)
GrR + rR == GrrRR | (ky3, dy3)
Grr == GrR | (ka1*L, da1)
Grrr == GrrR | (ka1*L, da1)
Grrrr == GrrrR | (ka1*L, da1)
GrR == GRR | (ka2*L, da2)
GrrR == GrRR | (ka2*L, da2)
GrrrR == GrrRR | (ka2*L, da2)
m = get_model()
show(m)
r > R | 1.0
R > r | 1.0
R > GR | 1.0
GR > R | 1.0
r > Gr | 1.0
Gr > r | 1.0
Gr > GR | 1.0
GR > Gr | 1.0
r + r > rr | 0.00020092425155716296
rr > r + r | 1.0
r + rr > rrr | 0.00020092425155716296
rrr > r + rr | 1.0
rr + r > rrr | 0.00020092425155716296
rrr > rr + r | 1.0
rr + rr > rrrr | 0.00020092425155716296
rrrr > rr + rr | 1.0
R + r > rR | 2.0092425155716294e-06
rR > R + r | 1.0
R + rr > rrR | 2.0092425155716294e-06
rrR > R + rr | 1.0
rR + r > rrR | 2.0092425155716294e-06
rrR > rR + r | 1.0
rR + rr > rrrR | 2.0092425155716294e-06
rrrR > rR + rr | 1.0
R + R > RR | 2.0092425155716296e-08
RR > R + R | 1.0
R + rR > rRR | 2.0092425155716296e-08
rRR > R + rR | 1.0
rR + R > rRR | 2.0092425155716296e-08
rRR > rR + R | 1.0
rR + rR > rrRR | 2.0092425155716296e-08
rrRR > rR + rR | 1.0
rr > rR | 0.01
rR > rr | 1.0
rrr > rrR | 0.01
rrR > rrr | 1.0
rrrr > rrrR | 0.01
rrrR > rrrr | 1.0
rR > RR | 0.01
RR > rR | 1.0
rrR > rRR | 0.01
rRR > rrR | 1.0
rrrR > rrRR | 0.01
rrRR > rrrR | 1.0
rr > Grr | 0.01
Grr > rr | 1.0
rrr > Grrr | 0.01
Grrr > rrr | 1.0
rrrr > Grrrr | 0.01
Grrrr > rrrr | 1.0
rR > GrR | 0.01
GrR > rR | 1.0
rrR > GrrR | 0.01
GrrR > rrR | 1.0
rrrR > GrrrR | 0.01
GrrrR > rrrR | 1.0
RR > GRR | 0.01
GRR > RR | 1.0
rRR > GrRR | 0.01
GrRR > rRR | 1.0
rrRR > GrrRR | 0.01
GrrRR > rrRR | 1.0
Gr + r > Grr | 0.00020092425155716296
Grr > Gr + r | 1.0
Gr + rr > Grrr | 0.00020092425155716296
Grrr > Gr + rr | 1.0
Grr + r > Grrr | 0.00020092425155716296
Grrr > Grr + r | 1.0
Grr + rr > Grrrr | 0.00020092425155716296
Grrrr > Grr + rr | 1.0
GR + r > GrR | 2.0092425155716294e-06
GrR > GR + r | 1.0
GR + rr > GrrR | 2.0092425155716294e-06
GrrR > GR + rr | 1.0
GrR + r > GrrR | 2.0092425155716294e-06
GrrR > GrR + r | 1.0
GrR + rr > GrrrR | 2.0092425155716294e-06
GrrrR > GrR + rr | 1.0
R + Gr > GrR | 2.0092425155716294e-06
GrR > R + Gr | 1.0
R + Grr > GrrR | 2.0092425155716294e-06
GrrR > R + Grr | 1.0
rR + Gr > GrrR | 2.0092425155716294e-06
GrrR > rR + Gr | 1.0
rR + Grr > GrrrR | 2.0092425155716294e-06
GrrrR > rR + Grr | 1.0
GR + R > GRR | 2.0092425155716296e-08
GRR > GR + R | 1.0
GR + rR > GrRR | 2.0092425155716296e-08
GrRR > GR + rR | 1.0
GrR + R > GrRR | 2.0092425155716296e-08
GrRR > GrR + R | 1.0
GrR + rR > GrrRR | 2.0092425155716296e-08
GrrRR > GrR + rR | 1.0
Grr > GrR | 0.01
GrR > Grr | 1.0
Grrr > GrrR | 0.01
GrrR > Grrr | 1.0
Grrrr > GrrrR | 0.01
GrrrR > Grrrr | 1.0
GrR > GRR | 0.01
GRR > GrR | 1.0
GrrR > GrRR | 0.01
GrRR > GrrR | 1.0
GrrrR > GrrRR | 0.01
GrrRR > GrrrR | 1.0
[17]:
obs0 = numpy.zeros(shape=(len(mols)))
obs0[0] = par.get_r0()
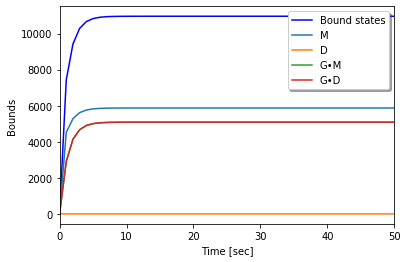
run_N2(m, mols, obs0)
Initial condition
r : 49770
rr : 0
rrr : 0
rrrr : 0
R : 0
rR : 0
rrR : 0
rrrR : 0
RR : 0
rRR : 0
rrRR : 0
Gr : 0
Grr : 0
Grrr : 0
Grrrr : 0
GR : 0
GrR : 0
GrrR : 0
GrrrR : 0
GRR : 0
GrRR : 0
GrrRR : 0
Trivalent model (N = 3 and kx > 0)¶
[18]:
# this is the trivalent model : N=3
N = 3.00
mols = ["r", "rr", "rrr", "rrrr", "rrrrr", "rrrrrr",
"R", "rR", "rrR", "rrrR", "rrrrR", "rrrrrR",
"RR", "rRR", "rrRR", "rrrRR", "rrrrRR",
"Gr", "Grr", "Grrr", "Grrrr", "Grrrrr", "Grrrrrr",
"GR", "GrR", "GrrR", "GrrrR", "GrrrrR", "GrrrrrR",
"GRR", "GrRR", "GrrRR", "GrrrRR", "GrrrrRR"]
[19]:
with reaction_rules():
# TCM (Ternary complex model)
r == R | (kl0*L, dl0)
R == GR | (ka0*G, da0)
r == Gr | (kg0*G, dg0)
Gr == GR | (kb0*L, db0)
# receptor dimerization
r + r == rr | (kx0, dx0)
r + rr == rrr | (kx0, dx0)
r + rrr == rrrr | (kx0, dx0)
rr + r == rrr | (kx0, dx0)
rr + rr == rrrr | (kx0, dx0)
rr + rrr == rrrrr | (kx0, dx0)
rrr + r == rrrr | (kx0, dx0)
rrr + rr == rrrrr | (kx0, dx0)
rrr + rrr == rrrrrr | (kx0, dx0)
R + r == rR | (kx1, dx1)
R + rr == rrR | (kx1, dx1)
R + rrr == rrrR | (kx1, dx1)
rR + r == rrR | (kx1, dx1)
rR + rr == rrrR | (kx1, dx1)
rR + rrr == rrrrR | (kx1, dx1)
rrR + r == rrrR | (kx1, dx1)
rrR + rr == rrrrR | (kx1, dx1)
rrR + rrr == rrrrrR | (kx1, dx1)
R + R == RR | (kx2, dx2)
R + rR == rRR | (kx2, dx2)
R + rrR == rrRR | (kx2, dx2)
rR + R == rRR | (kx2, dx2)
rR + rR == rrRR | (kx2, dx2)
rR + rrR == rrrRR | (kx2, dx2)
rrR + R == rrRR | (kx2, dx2)
rrR + rR == rrrRR | (kx2, dx2)
rrR + rrR == rrrrRR | (kx2, dx2)
rr == rR | (kl1*L, dl1)
rrr == rrR | (kl1*L, dl1)
rrrr == rrrR | (kl1*L, dl1)
rrrrr == rrrrR | (kl1*L, dl1)
rrrrrr == rrrrrR | (kl1*L, dl1)
rR == RR | (kl2*L, dl2)
rrR == rRR | (kl2*L, dl2)
rrrR == rrRR | (kl2*L, dl2)
rrrrR == rrrRR | (kl2*L, dl2)
rrrrrR == rrrrRR | (kl2*L, dl2)
# dimers coupled with G-proteins
rr == Grr | (kg1*G, dg1)
rrr == Grrr | (kg1*G, dg1)
rrrr == Grrrr | (kg1*G, dg1)
rrrrr == Grrrrr | (kg1*G, dg1)
rrrrrr == Grrrrrr | (kg1*G, dg1)
rR == GrR | (kb1*G, db1)
rrR == GrrR | (kb1*G, db1)
rrrR == GrrrR | (kb1*G, db1)
rrrrR == GrrrrR | (kb1*G, db1)
rrrrrR == GrrrrrR | (kb1*G, db1)
RR == GRR | (kb2*G, db2)
rRR == GrRR | (kb2*G, db2)
rrRR == GrrRR | (kb2*G, db2)
rrrRR == GrrrRR | (kb2*G, db2)
rrrrRR == GrrrrRR | (kb2*G, db2)
Gr + r == Grr | (ky0, dy0)
Gr + rr == Grrr | (ky0, dy0)
Gr + rrr == Grrrr | (ky0, dy0)
Grr + r == Grrr | (ky0, dy0)
Grr + rr == Grrrr | (ky0, dy0)
Grr + rrr == Grrrrr | (ky0, dy0)
Grrr + r == Grrrr | (ky0, dy0)
Grrr + rr == Grrrrr | (ky0, dy0)
Grrr + rrr == Grrrrrr | (ky0, dy0)
GR + r == GrR | (ky1, dy1)
GR + rr == GrrR | (ky1, dy1)
GR + rrr == GrrrR | (ky1, dy1)
GrR + r == GrrR | (ky1, dy1)
GrR + rr == GrrrR | (ky1, dy1)
GrR + rrr == GrrrrR | (ky1, dy1)
GrrR + r == GrrrR | (ky1, dy1)
GrrR + rr == GrrrrR | (ky1, dy1)
GrrR + rrr == GrrrrrR | (ky1, dy1)
R + Gr == GrR | (ky2, dy2)
R + Grr == GrrR | (ky2, dy2)
R + Grrr == GrrrR | (ky2, dy2)
rR + Gr == GrrR | (ky2, dy2)
rR + Grr == GrrrR | (ky2, dy2)
rR + Grrr == GrrrrR | (ky2, dy2)
rrR + Gr == GrrrR | (ky2, dy2)
rrR + Grr == GrrrrR | (ky2, dy2)
rrR + Grrr == GrrrrrR | (ky2, dy2)
GR + R == GRR | (ky3, dy3)
GR + rR == GrRR | (ky3, dy3)
GR + rrR == GrrRR | (ky3, dy3)
GrR + R == GrRR | (ky3, dy3)
GrR + rR == GrrRR | (ky3, dy3)
GrR + rrR == GrrrRR | (ky3, dy3)
GrrR + R == GrrRR | (ky3, dy3)
GrrR + rR == GrrrRR | (ky3, dy3)
GrrR + rrR == GrrrrRR | (ky3, dy3)
Grr == GrR | (ka1*L, da1)
Grrr == GrrR | (ka1*L, da1)
Grrrr == GrrrR | (ka1*L, da1)
Grrrrr == GrrrrR | (ka1*L, da1)
Grrrrrr == GrrrrrR | (ka1*L, da1)
GrR == GRR | (ka2*L, da2)
GrrR == GrRR | (ka2*L, da2)
GrrrR == GrrRR | (ka2*L, da2)
GrrrrR == GrrrRR | (ka2*L, da2)
GrrrrrR == GrrrrRR | (ka2*L, da2)
m = get_model()
show(m)
r > R | 1.0
R > r | 1.0
R > GR | 1.0
GR > R | 1.0
r > Gr | 1.0
Gr > r | 1.0
Gr > GR | 1.0
GR > Gr | 1.0
r + r > rr | 0.00020092425155716296
rr > r + r | 1.0
r + rr > rrr | 0.00020092425155716296
rrr > r + rr | 1.0
r + rrr > rrrr | 0.00020092425155716296
rrrr > r + rrr | 1.0
rr + r > rrr | 0.00020092425155716296
rrr > rr + r | 1.0
rr + rr > rrrr | 0.00020092425155716296
rrrr > rr + rr | 1.0
rr + rrr > rrrrr | 0.00020092425155716296
rrrrr > rr + rrr | 1.0
rrr + r > rrrr | 0.00020092425155716296
rrrr > rrr + r | 1.0
rrr + rr > rrrrr | 0.00020092425155716296
rrrrr > rrr + rr | 1.0
rrr + rrr > rrrrrr | 0.00020092425155716296
rrrrrr > rrr + rrr | 1.0
R + r > rR | 2.0092425155716294e-06
rR > R + r | 1.0
R + rr > rrR | 2.0092425155716294e-06
rrR > R + rr | 1.0
R + rrr > rrrR | 2.0092425155716294e-06
rrrR > R + rrr | 1.0
rR + r > rrR | 2.0092425155716294e-06
rrR > rR + r | 1.0
rR + rr > rrrR | 2.0092425155716294e-06
rrrR > rR + rr | 1.0
rR + rrr > rrrrR | 2.0092425155716294e-06
rrrrR > rR + rrr | 1.0
rrR + r > rrrR | 2.0092425155716294e-06
rrrR > rrR + r | 1.0
rrR + rr > rrrrR | 2.0092425155716294e-06
rrrrR > rrR + rr | 1.0
rrR + rrr > rrrrrR | 2.0092425155716294e-06
rrrrrR > rrR + rrr | 1.0
R + R > RR | 2.0092425155716296e-08
RR > R + R | 1.0
R + rR > rRR | 2.0092425155716296e-08
rRR > R + rR | 1.0
R + rrR > rrRR | 2.0092425155716296e-08
rrRR > R + rrR | 1.0
rR + R > rRR | 2.0092425155716296e-08
rRR > rR + R | 1.0
rR + rR > rrRR | 2.0092425155716296e-08
rrRR > rR + rR | 1.0
rR + rrR > rrrRR | 2.0092425155716296e-08
rrrRR > rR + rrR | 1.0
rrR + R > rrRR | 2.0092425155716296e-08
rrRR > rrR + R | 1.0
rrR + rR > rrrRR | 2.0092425155716296e-08
rrrRR > rrR + rR | 1.0
rrR + rrR > rrrrRR | 2.0092425155716296e-08
rrrrRR > rrR + rrR | 1.0
rr > rR | 0.01
rR > rr | 1.0
rrr > rrR | 0.01
rrR > rrr | 1.0
rrrr > rrrR | 0.01
rrrR > rrrr | 1.0
rrrrr > rrrrR | 0.01
rrrrR > rrrrr | 1.0
rrrrrr > rrrrrR | 0.01
rrrrrR > rrrrrr | 1.0
rR > RR | 0.01
RR > rR | 1.0
rrR > rRR | 0.01
rRR > rrR | 1.0
rrrR > rrRR | 0.01
rrRR > rrrR | 1.0
rrrrR > rrrRR | 0.01
rrrRR > rrrrR | 1.0
rrrrrR > rrrrRR | 0.01
rrrrRR > rrrrrR | 1.0
rr > Grr | 0.01
Grr > rr | 1.0
rrr > Grrr | 0.01
Grrr > rrr | 1.0
rrrr > Grrrr | 0.01
Grrrr > rrrr | 1.0
rrrrr > Grrrrr | 0.01
Grrrrr > rrrrr | 1.0
rrrrrr > Grrrrrr | 0.01
Grrrrrr > rrrrrr | 1.0
rR > GrR | 0.01
GrR > rR | 1.0
rrR > GrrR | 0.01
GrrR > rrR | 1.0
rrrR > GrrrR | 0.01
GrrrR > rrrR | 1.0
rrrrR > GrrrrR | 0.01
GrrrrR > rrrrR | 1.0
rrrrrR > GrrrrrR | 0.01
GrrrrrR > rrrrrR | 1.0
RR > GRR | 0.01
GRR > RR | 1.0
rRR > GrRR | 0.01
GrRR > rRR | 1.0
rrRR > GrrRR | 0.01
GrrRR > rrRR | 1.0
rrrRR > GrrrRR | 0.01
GrrrRR > rrrRR | 1.0
rrrrRR > GrrrrRR | 0.01
GrrrrRR > rrrrRR | 1.0
Gr + r > Grr | 0.00020092425155716296
Grr > Gr + r | 1.0
Gr + rr > Grrr | 0.00020092425155716296
Grrr > Gr + rr | 1.0
Gr + rrr > Grrrr | 0.00020092425155716296
Grrrr > Gr + rrr | 1.0
Grr + r > Grrr | 0.00020092425155716296
Grrr > Grr + r | 1.0
Grr + rr > Grrrr | 0.00020092425155716296
Grrrr > Grr + rr | 1.0
Grr + rrr > Grrrrr | 0.00020092425155716296
Grrrrr > Grr + rrr | 1.0
Grrr + r > Grrrr | 0.00020092425155716296
Grrrr > Grrr + r | 1.0
Grrr + rr > Grrrrr | 0.00020092425155716296
Grrrrr > Grrr + rr | 1.0
Grrr + rrr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grrr + rrr | 1.0
GR + r > GrR | 2.0092425155716294e-06
GrR > GR + r | 1.0
GR + rr > GrrR | 2.0092425155716294e-06
GrrR > GR + rr | 1.0
GR + rrr > GrrrR | 2.0092425155716294e-06
GrrrR > GR + rrr | 1.0
GrR + r > GrrR | 2.0092425155716294e-06
GrrR > GrR + r | 1.0
GrR + rr > GrrrR | 2.0092425155716294e-06
GrrrR > GrR + rr | 1.0
GrR + rrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrR + rrr | 1.0
GrrR + r > GrrrR | 2.0092425155716294e-06
GrrrR > GrrR + r | 1.0
GrrR + rr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrrR + rr | 1.0
GrrR + rrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrrR + rrr | 1.0
R + Gr > GrR | 2.0092425155716294e-06
GrR > R + Gr | 1.0
R + Grr > GrrR | 2.0092425155716294e-06
GrrR > R + Grr | 1.0
R + Grrr > GrrrR | 2.0092425155716294e-06
GrrrR > R + Grrr | 1.0
rR + Gr > GrrR | 2.0092425155716294e-06
GrrR > rR + Gr | 1.0
rR + Grr > GrrrR | 2.0092425155716294e-06
GrrrR > rR + Grr | 1.0
rR + Grrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rR + Grrr | 1.0
rrR + Gr > GrrrR | 2.0092425155716294e-06
GrrrR > rrR + Gr | 1.0
rrR + Grr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rrR + Grr | 1.0
rrR + Grrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rrR + Grrr | 1.0
GR + R > GRR | 2.0092425155716296e-08
GRR > GR + R | 1.0
GR + rR > GrRR | 2.0092425155716296e-08
GrRR > GR + rR | 1.0
GR + rrR > GrrRR | 2.0092425155716296e-08
GrrRR > GR + rrR | 1.0
GrR + R > GrRR | 2.0092425155716296e-08
GrRR > GrR + R | 1.0
GrR + rR > GrrRR | 2.0092425155716296e-08
GrrRR > GrR + rR | 1.0
GrR + rrR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrR + rrR | 1.0
GrrR + R > GrrRR | 2.0092425155716296e-08
GrrRR > GrrR + R | 1.0
GrrR + rR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrrR + rR | 1.0
GrrR + rrR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrrR + rrR | 1.0
Grr > GrR | 0.01
GrR > Grr | 1.0
Grrr > GrrR | 0.01
GrrR > Grrr | 1.0
Grrrr > GrrrR | 0.01
GrrrR > Grrrr | 1.0
Grrrrr > GrrrrR | 0.01
GrrrrR > Grrrrr | 1.0
Grrrrrr > GrrrrrR | 0.01
GrrrrrR > Grrrrrr | 1.0
GrR > GRR | 0.01
GRR > GrR | 1.0
GrrR > GrRR | 0.01
GrRR > GrrR | 1.0
GrrrR > GrrRR | 0.01
GrrRR > GrrrR | 1.0
GrrrrR > GrrrRR | 0.01
GrrrRR > GrrrrR | 1.0
GrrrrrR > GrrrrRR | 0.01
GrrrrRR > GrrrrrR | 1.0
[20]:
obs0 = numpy.zeros(shape=(len(mols)))
obs0[0] = par.get_r0()
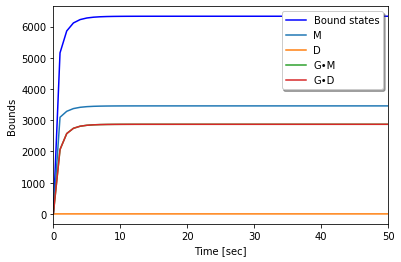
run_N3(m, mols, obs0)
Initial condition
r : 49770
rr : 0
rrr : 0
rrrr : 0
rrrrr : 0
rrrrrr : 0
R : 0
rR : 0
rrR : 0
rrrR : 0
rrrrR : 0
rrrrrR : 0
RR : 0
rRR : 0
rrRR : 0
rrrRR : 0
rrrrRR : 0
Gr : 0
Grr : 0
Grrr : 0
Grrrr : 0
Grrrrr : 0
Grrrrrr : 0
GR : 0
GrR : 0
GrrR : 0
GrrrR : 0
GrrrrR : 0
GrrrrrR : 0
GRR : 0
GrRR : 0
GrrRR : 0
GrrrRR : 0
GrrrrRR : 0
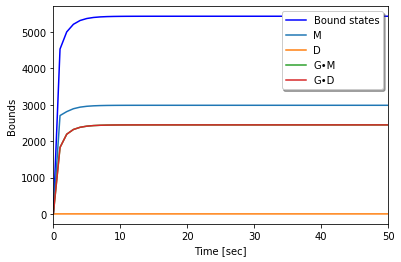
Tetravalent model (N = 4 and kx > 0)¶
[21]:
# this is the tetravalent model : N=4
N = 4.00
mols = ["r", "rr", "rrr", "rrrr", "rrrrr", "rrrrrr", "rrrrrrr", "rrrrrrrr",
"R", "rR", "rrR", "rrrR", "rrrrR", "rrrrrR", "rrrrrrR", "rrrrrrrR",
"RR", "rRR", "rrRR", "rrrRR", "rrrrRR", "rrrrrRR", "rrrrrrRR",
"Gr", "Grr", "Grrr", "Grrrr", "Grrrrr", "Grrrrrr", "Grrrrrrr", "Grrrrrrrr",
"GR", "GrR", "GrrR", "GrrrR", "GrrrrR", "GrrrrrR", "GrrrrrrR", "GrrrrrrrR",
"GRR", "GrRR", "GrrRR", "GrrrRR", "GrrrrRR", "GrrrrrRR", "GrrrrrrRR"]
[22]:
with reaction_rules():
# TCM (Ternary complex model)
r == R | (kl0*L, dl0)
R == GR | (ka0*G, da0)
r == Gr | (kg0*G, dg0)
Gr == GR | (kb0*L, db0)
# receptor dimerization
r + r == rr | (kx0, dx0)
r + rr == rrr | (kx0, dx0)
r + rrr == rrrr | (kx0, dx0)
r + rrrr == rrrrr | (kx0, dx0)
rr + r == rrr | (kx0, dx0)
rr + rr == rrrr | (kx0, dx0)
rr + rrr == rrrrr | (kx0, dx0)
rr + rrrr == rrrrrr | (kx0, dx0)
rrr + r == rrrr | (kx0, dx0)
rrr + rr == rrrrr | (kx0, dx0)
rrr + rrr == rrrrrr | (kx0, dx0)
rrr + rrrr == rrrrrrr | (kx0, dx0)
rrrr + r == rrrrr | (kx0, dx0)
rrrr + rr == rrrrrr | (kx0, dx0)
rrrr + rrr == rrrrrrr | (kx0, dx0)
rrrr + rrrr == rrrrrrrr | (kx0, dx0)
R + r == rR | (kx1, dx1)
R + rr == rrR | (kx1, dx1)
R + rrr == rrrR | (kx1, dx1)
R + rrrr == rrrrR | (kx1, dx1)
rR + r == rrR | (kx1, dx1)
rR + rr == rrrR | (kx1, dx1)
rR + rrr == rrrrR | (kx1, dx1)
rR + rrrr == rrrrrR | (kx1, dx1)
rrR + r == rrrR | (kx1, dx1)
rrR + rr == rrrrR | (kx1, dx1)
rrR + rrr == rrrrrR | (kx1, dx1)
rrR + rrrr == rrrrrrR | (kx1, dx1)
rrrR + r == rrrrR | (kx1, dx1)
rrrR + rr == rrrrrR | (kx1, dx1)
rrrR + rrr == rrrrrrR | (kx1, dx1)
rrrR + rrrr == rrrrrrrR | (kx1, dx1)
R + R == RR | (kx2, dx2)
R + rR == rRR | (kx2, dx2)
R + rrR == rrRR | (kx2, dx2)
R + rrrR == rrrRR | (kx2, dx2)
rR + R == rRR | (kx2, dx2)
rR + rR == rrRR | (kx2, dx2)
rR + rrR == rrrRR | (kx2, dx2)
rR + rrrR == rrrrRR | (kx2, dx2)
rrR + R == rrRR | (kx2, dx2)
rrR + rR == rrrRR | (kx2, dx2)
rrR + rrR == rrrrRR | (kx2, dx2)
rrR + rrrR == rrrrrRR | (kx2, dx2)
rrrR + R == rrrRR | (kx2, dx2)
rrrR + rR == rrrrRR | (kx2, dx2)
rrrR + rrR == rrrrrRR | (kx2, dx2)
rrrR + rrrR == rrrrrrRR | (kx2, dx2)
rr == rR | (kl1*L, dl1)
rrr == rrR | (kl1*L, dl1)
rrrr == rrrR | (kl1*L, dl1)
rrrrr == rrrrR | (kl1*L, dl1)
rrrrrr == rrrrrR | (kl1*L, dl1)
rrrrrrr == rrrrrrR | (kl1*L, dl1)
rrrrrrrr == rrrrrrrR | (kl1*L, dl1)
rR == RR | (kl2*L, dl2)
rrR == rRR | (kl2*L, dl2)
rrrR == rrRR | (kl2*L, dl2)
rrrrR == rrrRR | (kl2*L, dl2)
rrrrrR == rrrrRR | (kl2*L, dl2)
rrrrrrR == rrrrrRR | (kl2*L, dl2)
rrrrrrrR == rrrrrrRR | (kl2*L, dl2)
# dimers coupled with G-proteins
rr == Grr | (kg1*G, dg1)
rrr == Grrr | (kg1*G, dg1)
rrrr == Grrrr | (kg1*G, dg1)
rrrrr == Grrrrr | (kg1*G, dg1)
rrrrrr == Grrrrrr | (kg1*G, dg1)
rrrrrrr == Grrrrrrr | (kg1*G, dg1)
rrrrrrrr == Grrrrrrrr | (kg1*G, dg1)
rR == GrR | (kb1*G, db1)
rrR == GrrR | (kb1*G, db1)
rrrR == GrrrR | (kb1*G, db1)
rrrrR == GrrrrR | (kb1*G, db1)
rrrrrR == GrrrrrR | (kb1*G, db1)
rrrrrrR == GrrrrrrR | (kb1*G, db1)
rrrrrrrR == GrrrrrrrR | (kb1*G, db1)
RR == GRR | (kb2*G, db2)
rRR == GrRR | (kb2*G, db2)
rrRR == GrrRR | (kb2*G, db2)
rrrRR == GrrrRR | (kb2*G, db2)
rrrrRR == GrrrrRR | (kb2*G, db2)
rrrrrRR == GrrrrrRR | (kb2*G, db2)
rrrrrrRR == GrrrrrrRR | (kb2*G, db2)
Gr + r == Grr | (ky0, dy0)
Gr + rr == Grrr | (ky0, dy0)
Gr + rrr == Grrrr | (ky0, dy0)
Gr + rrrr == Grrrrr | (ky0, dy0)
Grr + r == Grrr | (ky0, dy0)
Grr + rr == Grrrr | (ky0, dy0)
Grr + rrr == Grrrrr | (ky0, dy0)
Grr + rrrr == Grrrrrr | (ky0, dy0)
Grrr + r == Grrrr | (ky0, dy0)
Grrr + rr == Grrrrr | (ky0, dy0)
Grrr + rrr == Grrrrrr | (ky0, dy0)
Grrr + rrrr == Grrrrrrr | (ky0, dy0)
Grrrr + r == Grrrrr | (ky0, dy0)
Grrrr + rr == Grrrrrr | (ky0, dy0)
Grrrr + rrr == Grrrrrrr | (ky0, dy0)
Grrrr + rrrr == Grrrrrrrr | (ky0, dy0)
GR + r == GrR | (ky1, dy1)
GR + rr == GrrR | (ky1, dy1)
GR + rrr == GrrrR | (ky1, dy1)
GR + rrrr == GrrrrR | (ky1, dy1)
GrR + r == GrrR | (ky1, dy1)
GrR + rr == GrrrR | (ky1, dy1)
GrR + rrr == GrrrrR | (ky1, dy1)
GrR + rrrr == GrrrrrR | (ky1, dy1)
GrrR + r == GrrrR | (ky1, dy1)
GrrR + rr == GrrrrR | (ky1, dy1)
GrrR + rrr == GrrrrrR | (ky1, dy1)
GrrR + rrrr == GrrrrrrR | (ky1, dy1)
GrrrR + r == GrrrrR | (ky1, dy1)
GrrrR + rr == GrrrrrR | (ky1, dy1)
GrrrR + rrr == GrrrrrrR | (ky1, dy1)
GrrrR + rrrr == GrrrrrrrR | (ky1, dy1)
R + Gr == GrR | (ky2, dy2)
R + Grr == GrrR | (ky2, dy2)
R + Grrr == GrrrR | (ky2, dy2)
R + Grrrr == GrrrrR | (ky2, dy2)
rR + Gr == GrrR | (ky2, dy2)
rR + Grr == GrrrR | (ky2, dy2)
rR + Grrr == GrrrrR | (ky2, dy2)
rR + Grrrr == GrrrrrR | (ky2, dy2)
rrR + Gr == GrrrR | (ky2, dy2)
rrR + Grr == GrrrrR | (ky2, dy2)
rrR + Grrr == GrrrrrR | (ky2, dy2)
rrR + Grrrr == GrrrrrrR | (ky2, dy2)
rrrR + Gr == GrrrrR | (ky2, dy2)
rrrR + Grr == GrrrrrR | (ky2, dy2)
rrrR + Grrr == GrrrrrrR | (ky2, dy2)
rrrR + Grrrr == GrrrrrrrR | (ky2, dy2)
GR + R == GRR | (ky3, dy3)
GR + rR == GrRR | (ky3, dy3)
GR + rrR == GrrRR | (ky3, dy3)
GR + rrrR == GrrrRR | (ky3, dy3)
GrR + R == GrRR | (ky3, dy3)
GrR + rR == GrrRR | (ky3, dy3)
GrR + rrR == GrrrRR | (ky3, dy3)
GrR + rrrR == GrrrrRR | (ky3, dy3)
GrrR + R == GrrRR | (ky3, dy3)
GrrR + rR == GrrrRR | (ky3, dy3)
GrrR + rrR == GrrrrRR | (ky3, dy3)
GrrR + rrrR == GrrrrrRR | (ky3, dy3)
GrrrR + R == GrrrRR | (ky3, dy3)
GrrrR + rR == GrrrrRR | (ky3, dy3)
GrrrR + rrR == GrrrrrRR | (ky3, dy3)
GrrrR + rrrR == GrrrrrrRR | (ky3, dy3)
Grr == GrR | (ka1*L, da1)
Grrr == GrrR | (ka1*L, da1)
Grrrr == GrrrR | (ka1*L, da1)
Grrrrr == GrrrrR | (ka1*L, da1)
Grrrrrr == GrrrrrR | (ka1*L, da1)
Grrrrrrr == GrrrrrrR | (ka1*L, da1)
Grrrrrrrr == GrrrrrrrR | (ka1*L, da1)
GrR == GRR | (ka2*L, da2)
GrrR == GrRR | (ka2*L, da2)
GrrrR == GrrRR | (ka2*L, da2)
GrrrrR == GrrrRR | (ka2*L, da2)
GrrrrrR == GrrrrRR | (ka2*L, da2)
GrrrrrrR == GrrrrrRR | (ka2*L, da2)
GrrrrrrrR == GrrrrrrRR | (ka2*L, da2)
m = get_model()
show(m)
r > R | 1.0
R > r | 1.0
R > GR | 1.0
GR > R | 1.0
r > Gr | 1.0
Gr > r | 1.0
Gr > GR | 1.0
GR > Gr | 1.0
r + r > rr | 0.00020092425155716296
rr > r + r | 1.0
r + rr > rrr | 0.00020092425155716296
rrr > r + rr | 1.0
r + rrr > rrrr | 0.00020092425155716296
rrrr > r + rrr | 1.0
r + rrrr > rrrrr | 0.00020092425155716296
rrrrr > r + rrrr | 1.0
rr + r > rrr | 0.00020092425155716296
rrr > rr + r | 1.0
rr + rr > rrrr | 0.00020092425155716296
rrrr > rr + rr | 1.0
rr + rrr > rrrrr | 0.00020092425155716296
rrrrr > rr + rrr | 1.0
rr + rrrr > rrrrrr | 0.00020092425155716296
rrrrrr > rr + rrrr | 1.0
rrr + r > rrrr | 0.00020092425155716296
rrrr > rrr + r | 1.0
rrr + rr > rrrrr | 0.00020092425155716296
rrrrr > rrr + rr | 1.0
rrr + rrr > rrrrrr | 0.00020092425155716296
rrrrrr > rrr + rrr | 1.0
rrr + rrrr > rrrrrrr | 0.00020092425155716296
rrrrrrr > rrr + rrrr | 1.0
rrrr + r > rrrrr | 0.00020092425155716296
rrrrr > rrrr + r | 1.0
rrrr + rr > rrrrrr | 0.00020092425155716296
rrrrrr > rrrr + rr | 1.0
rrrr + rrr > rrrrrrr | 0.00020092425155716296
rrrrrrr > rrrr + rrr | 1.0
rrrr + rrrr > rrrrrrrr | 0.00020092425155716296
rrrrrrrr > rrrr + rrrr | 1.0
R + r > rR | 2.0092425155716294e-06
rR > R + r | 1.0
R + rr > rrR | 2.0092425155716294e-06
rrR > R + rr | 1.0
R + rrr > rrrR | 2.0092425155716294e-06
rrrR > R + rrr | 1.0
R + rrrr > rrrrR | 2.0092425155716294e-06
rrrrR > R + rrrr | 1.0
rR + r > rrR | 2.0092425155716294e-06
rrR > rR + r | 1.0
rR + rr > rrrR | 2.0092425155716294e-06
rrrR > rR + rr | 1.0
rR + rrr > rrrrR | 2.0092425155716294e-06
rrrrR > rR + rrr | 1.0
rR + rrrr > rrrrrR | 2.0092425155716294e-06
rrrrrR > rR + rrrr | 1.0
rrR + r > rrrR | 2.0092425155716294e-06
rrrR > rrR + r | 1.0
rrR + rr > rrrrR | 2.0092425155716294e-06
rrrrR > rrR + rr | 1.0
rrR + rrr > rrrrrR | 2.0092425155716294e-06
rrrrrR > rrR + rrr | 1.0
rrR + rrrr > rrrrrrR | 2.0092425155716294e-06
rrrrrrR > rrR + rrrr | 1.0
rrrR + r > rrrrR | 2.0092425155716294e-06
rrrrR > rrrR + r | 1.0
rrrR + rr > rrrrrR | 2.0092425155716294e-06
rrrrrR > rrrR + rr | 1.0
rrrR + rrr > rrrrrrR | 2.0092425155716294e-06
rrrrrrR > rrrR + rrr | 1.0
rrrR + rrrr > rrrrrrrR | 2.0092425155716294e-06
rrrrrrrR > rrrR + rrrr | 1.0
R + R > RR | 2.0092425155716296e-08
RR > R + R | 1.0
R + rR > rRR | 2.0092425155716296e-08
rRR > R + rR | 1.0
R + rrR > rrRR | 2.0092425155716296e-08
rrRR > R + rrR | 1.0
R + rrrR > rrrRR | 2.0092425155716296e-08
rrrRR > R + rrrR | 1.0
rR + R > rRR | 2.0092425155716296e-08
rRR > rR + R | 1.0
rR + rR > rrRR | 2.0092425155716296e-08
rrRR > rR + rR | 1.0
rR + rrR > rrrRR | 2.0092425155716296e-08
rrrRR > rR + rrR | 1.0
rR + rrrR > rrrrRR | 2.0092425155716296e-08
rrrrRR > rR + rrrR | 1.0
rrR + R > rrRR | 2.0092425155716296e-08
rrRR > rrR + R | 1.0
rrR + rR > rrrRR | 2.0092425155716296e-08
rrrRR > rrR + rR | 1.0
rrR + rrR > rrrrRR | 2.0092425155716296e-08
rrrrRR > rrR + rrR | 1.0
rrR + rrrR > rrrrrRR | 2.0092425155716296e-08
rrrrrRR > rrR + rrrR | 1.0
rrrR + R > rrrRR | 2.0092425155716296e-08
rrrRR > rrrR + R | 1.0
rrrR + rR > rrrrRR | 2.0092425155716296e-08
rrrrRR > rrrR + rR | 1.0
rrrR + rrR > rrrrrRR | 2.0092425155716296e-08
rrrrrRR > rrrR + rrR | 1.0
rrrR + rrrR > rrrrrrRR | 2.0092425155716296e-08
rrrrrrRR > rrrR + rrrR | 1.0
rr > rR | 0.01
rR > rr | 1.0
rrr > rrR | 0.01
rrR > rrr | 1.0
rrrr > rrrR | 0.01
rrrR > rrrr | 1.0
rrrrr > rrrrR | 0.01
rrrrR > rrrrr | 1.0
rrrrrr > rrrrrR | 0.01
rrrrrR > rrrrrr | 1.0
rrrrrrr > rrrrrrR | 0.01
rrrrrrR > rrrrrrr | 1.0
rrrrrrrr > rrrrrrrR | 0.01
rrrrrrrR > rrrrrrrr | 1.0
rR > RR | 0.01
RR > rR | 1.0
rrR > rRR | 0.01
rRR > rrR | 1.0
rrrR > rrRR | 0.01
rrRR > rrrR | 1.0
rrrrR > rrrRR | 0.01
rrrRR > rrrrR | 1.0
rrrrrR > rrrrRR | 0.01
rrrrRR > rrrrrR | 1.0
rrrrrrR > rrrrrRR | 0.01
rrrrrRR > rrrrrrR | 1.0
rrrrrrrR > rrrrrrRR | 0.01
rrrrrrRR > rrrrrrrR | 1.0
rr > Grr | 0.01
Grr > rr | 1.0
rrr > Grrr | 0.01
Grrr > rrr | 1.0
rrrr > Grrrr | 0.01
Grrrr > rrrr | 1.0
rrrrr > Grrrrr | 0.01
Grrrrr > rrrrr | 1.0
rrrrrr > Grrrrrr | 0.01
Grrrrrr > rrrrrr | 1.0
rrrrrrr > Grrrrrrr | 0.01
Grrrrrrr > rrrrrrr | 1.0
rrrrrrrr > Grrrrrrrr | 0.01
Grrrrrrrr > rrrrrrrr | 1.0
rR > GrR | 0.01
GrR > rR | 1.0
rrR > GrrR | 0.01
GrrR > rrR | 1.0
rrrR > GrrrR | 0.01
GrrrR > rrrR | 1.0
rrrrR > GrrrrR | 0.01
GrrrrR > rrrrR | 1.0
rrrrrR > GrrrrrR | 0.01
GrrrrrR > rrrrrR | 1.0
rrrrrrR > GrrrrrrR | 0.01
GrrrrrrR > rrrrrrR | 1.0
rrrrrrrR > GrrrrrrrR | 0.01
GrrrrrrrR > rrrrrrrR | 1.0
RR > GRR | 0.01
GRR > RR | 1.0
rRR > GrRR | 0.01
GrRR > rRR | 1.0
rrRR > GrrRR | 0.01
GrrRR > rrRR | 1.0
rrrRR > GrrrRR | 0.01
GrrrRR > rrrRR | 1.0
rrrrRR > GrrrrRR | 0.01
GrrrrRR > rrrrRR | 1.0
rrrrrRR > GrrrrrRR | 0.01
GrrrrrRR > rrrrrRR | 1.0
rrrrrrRR > GrrrrrrRR | 0.01
GrrrrrrRR > rrrrrrRR | 1.0
Gr + r > Grr | 0.00020092425155716296
Grr > Gr + r | 1.0
Gr + rr > Grrr | 0.00020092425155716296
Grrr > Gr + rr | 1.0
Gr + rrr > Grrrr | 0.00020092425155716296
Grrrr > Gr + rrr | 1.0
Gr + rrrr > Grrrrr | 0.00020092425155716296
Grrrrr > Gr + rrrr | 1.0
Grr + r > Grrr | 0.00020092425155716296
Grrr > Grr + r | 1.0
Grr + rr > Grrrr | 0.00020092425155716296
Grrrr > Grr + rr | 1.0
Grr + rrr > Grrrrr | 0.00020092425155716296
Grrrrr > Grr + rrr | 1.0
Grr + rrrr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grr + rrrr | 1.0
Grrr + r > Grrrr | 0.00020092425155716296
Grrrr > Grrr + r | 1.0
Grrr + rr > Grrrrr | 0.00020092425155716296
Grrrrr > Grrr + rr | 1.0
Grrr + rrr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grrr + rrr | 1.0
Grrr + rrrr > Grrrrrrr | 0.00020092425155716296
Grrrrrrr > Grrr + rrrr | 1.0
Grrrr + r > Grrrrr | 0.00020092425155716296
Grrrrr > Grrrr + r | 1.0
Grrrr + rr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grrrr + rr | 1.0
Grrrr + rrr > Grrrrrrr | 0.00020092425155716296
Grrrrrrr > Grrrr + rrr | 1.0
Grrrr + rrrr > Grrrrrrrr | 0.00020092425155716296
Grrrrrrrr > Grrrr + rrrr | 1.0
GR + r > GrR | 2.0092425155716294e-06
GrR > GR + r | 1.0
GR + rr > GrrR | 2.0092425155716294e-06
GrrR > GR + rr | 1.0
GR + rrr > GrrrR | 2.0092425155716294e-06
GrrrR > GR + rrr | 1.0
GR + rrrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GR + rrrr | 1.0
GrR + r > GrrR | 2.0092425155716294e-06
GrrR > GrR + r | 1.0
GrR + rr > GrrrR | 2.0092425155716294e-06
GrrrR > GrR + rr | 1.0
GrR + rrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrR + rrr | 1.0
GrR + rrrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrR + rrrr | 1.0
GrrR + r > GrrrR | 2.0092425155716294e-06
GrrrR > GrrR + r | 1.0
GrrR + rr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrrR + rr | 1.0
GrrR + rrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrrR + rrr | 1.0
GrrR + rrrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > GrrR + rrrr | 1.0
GrrrR + r > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrrrR + r | 1.0
GrrrR + rr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrrrR + rr | 1.0
GrrrR + rrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > GrrrR + rrr | 1.0
GrrrR + rrrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > GrrrR + rrrr | 1.0
R + Gr > GrR | 2.0092425155716294e-06
GrR > R + Gr | 1.0
R + Grr > GrrR | 2.0092425155716294e-06
GrrR > R + Grr | 1.0
R + Grrr > GrrrR | 2.0092425155716294e-06
GrrrR > R + Grrr | 1.0
R + Grrrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > R + Grrrr | 1.0
rR + Gr > GrrR | 2.0092425155716294e-06
GrrR > rR + Gr | 1.0
rR + Grr > GrrrR | 2.0092425155716294e-06
GrrrR > rR + Grr | 1.0
rR + Grrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rR + Grrr | 1.0
rR + Grrrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rR + Grrrr | 1.0
rrR + Gr > GrrrR | 2.0092425155716294e-06
GrrrR > rrR + Gr | 1.0
rrR + Grr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rrR + Grr | 1.0
rrR + Grrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rrR + Grrr | 1.0
rrR + Grrrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > rrR + Grrrr | 1.0
rrrR + Gr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rrrR + Gr | 1.0
rrrR + Grr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rrrR + Grr | 1.0
rrrR + Grrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > rrrR + Grrr | 1.0
rrrR + Grrrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > rrrR + Grrrr | 1.0
GR + R > GRR | 2.0092425155716296e-08
GRR > GR + R | 1.0
GR + rR > GrRR | 2.0092425155716296e-08
GrRR > GR + rR | 1.0
GR + rrR > GrrRR | 2.0092425155716296e-08
GrrRR > GR + rrR | 1.0
GR + rrrR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GR + rrrR | 1.0
GrR + R > GrRR | 2.0092425155716296e-08
GrRR > GrR + R | 1.0
GrR + rR > GrrRR | 2.0092425155716296e-08
GrrRR > GrR + rR | 1.0
GrR + rrR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrR + rrR | 1.0
GrR + rrrR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrR + rrrR | 1.0
GrrR + R > GrrRR | 2.0092425155716296e-08
GrrRR > GrrR + R | 1.0
GrrR + rR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrrR + rR | 1.0
GrrR + rrR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrrR + rrR | 1.0
GrrR + rrrR > GrrrrrRR | 2.0092425155716296e-08
GrrrrrRR > GrrR + rrrR | 1.0
GrrrR + R > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrrrR + R | 1.0
GrrrR + rR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrrrR + rR | 1.0
GrrrR + rrR > GrrrrrRR | 2.0092425155716296e-08
GrrrrrRR > GrrrR + rrR | 1.0
GrrrR + rrrR > GrrrrrrRR | 2.0092425155716296e-08
GrrrrrrRR > GrrrR + rrrR | 1.0
Grr > GrR | 0.01
GrR > Grr | 1.0
Grrr > GrrR | 0.01
GrrR > Grrr | 1.0
Grrrr > GrrrR | 0.01
GrrrR > Grrrr | 1.0
Grrrrr > GrrrrR | 0.01
GrrrrR > Grrrrr | 1.0
Grrrrrr > GrrrrrR | 0.01
GrrrrrR > Grrrrrr | 1.0
Grrrrrrr > GrrrrrrR | 0.01
GrrrrrrR > Grrrrrrr | 1.0
Grrrrrrrr > GrrrrrrrR | 0.01
GrrrrrrrR > Grrrrrrrr | 1.0
GrR > GRR | 0.01
GRR > GrR | 1.0
GrrR > GrRR | 0.01
GrRR > GrrR | 1.0
GrrrR > GrrRR | 0.01
GrrRR > GrrrR | 1.0
GrrrrR > GrrrRR | 0.01
GrrrRR > GrrrrR | 1.0
GrrrrrR > GrrrrRR | 0.01
GrrrrRR > GrrrrrR | 1.0
GrrrrrrR > GrrrrrRR | 0.01
GrrrrrRR > GrrrrrrR | 1.0
GrrrrrrrR > GrrrrrrRR | 0.01
GrrrrrrRR > GrrrrrrrR | 1.0
[23]:
obs0 = numpy.zeros(shape=(len(mols)))
obs0[0] = par.get_r0()
run_N4(m, mols, obs0)
Initial condition
r : 49770
rr : 0
rrr : 0
rrrr : 0
rrrrr : 0
rrrrrr : 0
rrrrrrr : 0
rrrrrrrr : 0
R : 0
rR : 0
rrR : 0
rrrR : 0
rrrrR : 0
rrrrrR : 0
rrrrrrR : 0
rrrrrrrR : 0
RR : 0
rRR : 0
rrRR : 0
rrrRR : 0
rrrrRR : 0
rrrrrRR : 0
rrrrrrRR : 0
Gr : 0
Grr : 0
Grrr : 0
Grrrr : 0
Grrrrr : 0
Grrrrrr : 0
Grrrrrrr : 0
Grrrrrrrr : 0
GR : 0
GrR : 0
GrrR : 0
GrrrR : 0
GrrrrR : 0
GrrrrrR : 0
GrrrrrrR : 0
GrrrrrrrR : 0
GRR : 0
GrRR : 0
GrrRR : 0
GrrrRR : 0
GrrrrRR : 0
GrrrrrRR : 0
GrrrrrrRR : 0
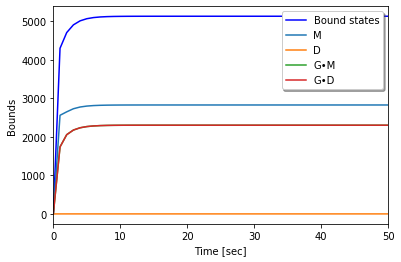
Pentavalent model (N = 5 and kx > 0)¶
[24]:
# this is the pentavalent model : N=5
N = 5.00
mols = ["r", "rr", "rrr", "rrrr", "rrrrr", "rrrrrr", "rrrrrrr", "rrrrrrrr", "rrrrrrrr", "rrrrrrrrrr",
"R", "rR", "rrR", "rrrR", "rrrrR", "rrrrrR", "rrrrrrR", "rrrrrrrR", "rrrrrrrR", "rrrrrrrrrR",
"RR", "rRR", "rrRR", "rrrRR", "rrrrRR", "rrrrrRR", "rrrrrrRR", "rrrrrrRR", "rrrrrrrrRR",
"Gr", "Grr", "Grrr", "Grrrr", "Grrrrr", "Grrrrrr", "Grrrrrrr", "Grrrrrrrr", "Grrrrrrrr", "Grrrrrrrrrr",
"GR", "GrR", "GrrR", "GrrrR", "GrrrrR", "GrrrrrR", "GrrrrrrR", "GrrrrrrrR", "GrrrrrrrR", "GrrrrrrrrrR",
"GRR", "GrRR", "GrrRR", "GrrrRR", "GrrrrRR", "GrrrrrRR", "GrrrrrrRR", "GrrrrrrRR", "GrrrrrrrrRR"]
[25]:
with reaction_rules():
# TCM (Ternary complex model)
r == R | (kl0*L, dl0)
R == GR | (ka0*G, da0)
r == Gr | (kg0*G, dg0)
Gr == GR | (kb0*L, db0)
# receptor dimerization
r + r == rr | (kx0, dx0)
r + rr == rrr | (kx0, dx0)
r + rrr == rrrr | (kx0, dx0)
r + rrrr == rrrrr | (kx0, dx0)
r + rrrrr == rrrrrr | (kx0, dx0)
rr + r == rrr | (kx0, dx0)
rr + rr == rrrr | (kx0, dx0)
rr + rrr == rrrrr | (kx0, dx0)
rr + rrrr == rrrrrr | (kx0, dx0)
rr + rrrrr == rrrrrrr | (kx0, dx0)
rrr + r == rrrr | (kx0, dx0)
rrr + rr == rrrrr | (kx0, dx0)
rrr + rrr == rrrrrr | (kx0, dx0)
rrr + rrrr == rrrrrrr | (kx0, dx0)
rrr + rrrrr == rrrrrrrr | (kx0, dx0)
rrrr + r == rrrrr | (kx0, dx0)
rrrr + rr == rrrrrr | (kx0, dx0)
rrrr + rrr == rrrrrrr | (kx0, dx0)
rrrr + rrrr == rrrrrrrr | (kx0, dx0)
rrrr + rrrrr == rrrrrrrrr | (kx0, dx0)
rrrrr + r == rrrrrr | (kx0, dx0)
rrrrr + rr == rrrrrrr | (kx0, dx0)
rrrrr + rrr == rrrrrrrr | (kx0, dx0)
rrrrr + rrrr == rrrrrrrrr | (kx0, dx0)
rrrrr + rrrrr == rrrrrrrrrr | (kx0, dx0)
R + r == rR | (kx1, dx1)
R + rr == rrR | (kx1, dx1)
R + rrr == rrrR | (kx1, dx1)
R + rrrr == rrrrR | (kx1, dx1)
R + rrrrr == rrrrrR | (kx1, dx1)
rR + r == rrR | (kx1, dx1)
rR + rr == rrrR | (kx1, dx1)
rR + rrr == rrrrR | (kx1, dx1)
rR + rrrr == rrrrrR | (kx1, dx1)
rR + rrrrr == rrrrrrR | (kx1, dx1)
rrR + r == rrrR | (kx1, dx1)
rrR + rr == rrrrR | (kx1, dx1)
rrR + rrr == rrrrrR | (kx1, dx1)
rrR + rrrr == rrrrrrR | (kx1, dx1)
rrR + rrrrr == rrrrrrrR | (kx1, dx1)
rrrR + r == rrrrR | (kx1, dx1)
rrrR + rr == rrrrrR | (kx1, dx1)
rrrR + rrr == rrrrrrR | (kx1, dx1)
rrrR + rrrr == rrrrrrrR | (kx1, dx1)
rrrR + rrrrr == rrrrrrrrR | (kx1, dx1)
rrrrR + r == rrrrrR | (kx1, dx1)
rrrrR + rr == rrrrrrR | (kx1, dx1)
rrrrR + rrr == rrrrrrrR | (kx1, dx1)
rrrrR + rrrr == rrrrrrrrR | (kx1, dx1)
rrrrR + rrrrr == rrrrrrrrrR | (kx1, dx1)
R + R == RR | (kx2, dx2)
R + rR == rRR | (kx2, dx2)
R + rrR == rrRR | (kx2, dx2)
R + rrrR == rrrRR | (kx2, dx2)
R + rrrrR == rrrrRR | (kx2, dx2)
rR + R == rRR | (kx2, dx2)
rR + rR == rrRR | (kx2, dx2)
rR + rrR == rrrRR | (kx2, dx2)
rR + rrrR == rrrrRR | (kx2, dx2)
rR + rrrrR == rrrrrRR | (kx2, dx2)
rrR + R == rrRR | (kx2, dx2)
rrR + rR == rrrRR | (kx2, dx2)
rrR + rrR == rrrrRR | (kx2, dx2)
rrR + rrrR == rrrrrRR | (kx2, dx2)
rrR + rrrrR == rrrrrrRR | (kx2, dx2)
rrrR + R == rrrRR | (kx2, dx2)
rrrR + rR == rrrrRR | (kx2, dx2)
rrrR + rrR == rrrrrRR | (kx2, dx2)
rrrR + rrrR == rrrrrrRR | (kx2, dx2)
rrrR + rrrrR == rrrrrrrRR | (kx2, dx2)
rrrrR + R == rrrrRR | (kx2, dx2)
rrrrR + rR == rrrrrRR | (kx2, dx2)
rrrrR + rrR == rrrrrrRR | (kx2, dx2)
rrrrR + rrrR == rrrrrrrRR | (kx2, dx2)
rrrrR + rrrrR == rrrrrrrrRR | (kx2, dx2)
rr == rR | (kl1*L, dl1)
rrr == rrR | (kl1*L, dl1)
rrrr == rrrR | (kl1*L, dl1)
rrrrr == rrrrR | (kl1*L, dl1)
rrrrrr == rrrrrR | (kl1*L, dl1)
rrrrrrr == rrrrrrR | (kl1*L, dl1)
rrrrrrrr == rrrrrrrR | (kl1*L, dl1)
rrrrrrrrr == rrrrrrrrR | (kl1*L, dl1)
rrrrrrrrrr == rrrrrrrrrR | (kl1*L, dl1)
rR == RR | (kl2*L, dl2)
rrR == rRR | (kl2*L, dl2)
rrrR == rrRR | (kl2*L, dl2)
rrrrR == rrrRR | (kl2*L, dl2)
rrrrrR == rrrrRR | (kl2*L, dl2)
rrrrrrR == rrrrrRR | (kl2*L, dl2)
rrrrrrrR == rrrrrrRR | (kl2*L, dl2)
rrrrrrrrR == rrrrrrrRR | (kl2*L, dl2)
rrrrrrrrrR == rrrrrrrrRR | (kl2*L, dl2)
# dimers coupled with G-proteins
rr == Grr | (kg1*G, dg1)
rrr == Grrr | (kg1*G, dg1)
rrrr == Grrrr | (kg1*G, dg1)
rrrrr == Grrrrr | (kg1*G, dg1)
rrrrrr == Grrrrrr | (kg1*G, dg1)
rrrrrrr == Grrrrrrr | (kg1*G, dg1)
rrrrrrrr == Grrrrrrrr | (kg1*G, dg1)
rrrrrrrrr == Grrrrrrrrr | (kg1*G, dg1)
rrrrrrrrrr == Grrrrrrrrrr | (kg1*G, dg1)
rR == GrR | (kb1*G, db1)
rrR == GrrR | (kb1*G, db1)
rrrR == GrrrR | (kb1*G, db1)
rrrrR == GrrrrR | (kb1*G, db1)
rrrrrR == GrrrrrR | (kb1*G, db1)
rrrrrrR == GrrrrrrR | (kb1*G, db1)
rrrrrrrR == GrrrrrrrR | (kb1*G, db1)
rrrrrrrrR == GrrrrrrrrR | (kb1*G, db1)
rrrrrrrrrR == GrrrrrrrrrR | (kb1*G, db1)
RR == GRR | (kb2*G, db2)
rRR == GrRR | (kb2*G, db2)
rrRR == GrrRR | (kb2*G, db2)
rrrRR == GrrrRR | (kb2*G, db2)
rrrrRR == GrrrrRR | (kb2*G, db2)
rrrrrRR == GrrrrrRR | (kb2*G, db2)
rrrrrrRR == GrrrrrrRR | (kb2*G, db2)
rrrrrrrRR == GrrrrrrrRR | (kb2*G, db2)
rrrrrrrrRR == GrrrrrrrrRR | (kb2*G, db2)
Gr + r == Grr | (ky0, dy0)
Gr + rr == Grrr | (ky0, dy0)
Gr + rrr == Grrrr | (ky0, dy0)
Gr + rrrr == Grrrrr | (ky0, dy0)
Gr + rrrrr == Grrrrrr | (ky0, dy0)
Grr + r == Grrr | (ky0, dy0)
Grr + rr == Grrrr | (ky0, dy0)
Grr + rrr == Grrrrr | (ky0, dy0)
Grr + rrrr == Grrrrrr | (ky0, dy0)
Grr + rrrrr == Grrrrrrr | (ky0, dy0)
Grrr + r == Grrrr | (ky0, dy0)
Grrr + rr == Grrrrr | (ky0, dy0)
Grrr + rrr == Grrrrrr | (ky0, dy0)
Grrr + rrrr == Grrrrrrr | (ky0, dy0)
Grrr + rrrrr == Grrrrrrrr | (ky0, dy0)
Grrrr + r == Grrrrr | (ky0, dy0)
Grrrr + rr == Grrrrrr | (ky0, dy0)
Grrrr + rrr == Grrrrrrr | (ky0, dy0)
Grrrr + rrrr == Grrrrrrrr | (ky0, dy0)
Grrrr + rrrrr == Grrrrrrrrr | (ky0, dy0)
Grrrrr + r == Grrrrrr | (ky0, dy0)
Grrrrr + rr == Grrrrrrr | (ky0, dy0)
Grrrrr + rrr == Grrrrrrrr | (ky0, dy0)
Grrrrr + rrrr == Grrrrrrrrr | (ky0, dy0)
Grrrrr + rrrrr == Grrrrrrrrrr | (ky0, dy0)
GR + r == GrR | (ky1, dy1)
GR + rr == GrrR | (ky1, dy1)
GR + rrr == GrrrR | (ky1, dy1)
GR + rrrr == GrrrrR | (ky1, dy1)
GR + rrrrr == GrrrrrR | (ky1, dy1)
GrR + r == GrrR | (ky1, dy1)
GrR + rr == GrrrR | (ky1, dy1)
GrR + rrr == GrrrrR | (ky1, dy1)
GrR + rrrr == GrrrrrR | (ky1, dy1)
GrR + rrrrr == GrrrrrrR | (ky1, dy1)
GrrR + r == GrrrR | (ky1, dy1)
GrrR + rr == GrrrrR | (ky1, dy1)
GrrR + rrr == GrrrrrR | (ky1, dy1)
GrrR + rrrr == GrrrrrrR | (ky1, dy1)
GrrR + rrrrr == GrrrrrrrR | (ky1, dy1)
GrrrR + r == GrrrrR | (ky1, dy1)
GrrrR + rr == GrrrrrR | (ky1, dy1)
GrrrR + rrr == GrrrrrrR | (ky1, dy1)
GrrrR + rrrr == GrrrrrrrR | (ky1, dy1)
GrrrR + rrrrr == GrrrrrrrrR | (ky1, dy1)
GrrrrR + r == GrrrrrR | (ky1, dy1)
GrrrrR + rr == GrrrrrrR | (ky1, dy1)
GrrrrR + rrr == GrrrrrrrR | (ky1, dy1)
GrrrrR + rrrr == GrrrrrrrrR | (ky1, dy1)
GrrrrR + rrrrr == GrrrrrrrrrR | (ky1, dy1)
R + Gr == GrR | (ky2, dy2)
R + Grr == GrrR | (ky2, dy2)
R + Grrr == GrrrR | (ky2, dy2)
R + Grrrr == GrrrrR | (ky2, dy2)
R + Grrrrr == GrrrrrR | (ky2, dy2)
rR + Gr == GrrR | (ky2, dy2)
rR + Grr == GrrrR | (ky2, dy2)
rR + Grrr == GrrrrR | (ky2, dy2)
rR + Grrrr == GrrrrrR | (ky2, dy2)
rR + Grrrrr == GrrrrrrR | (ky2, dy2)
rrR + Gr == GrrrR | (ky2, dy2)
rrR + Grr == GrrrrR | (ky2, dy2)
rrR + Grrr == GrrrrrR | (ky2, dy2)
rrR + Grrrr == GrrrrrrR | (ky2, dy2)
rrR + Grrrrr == GrrrrrrrR | (ky2, dy2)
rrrR + Gr == GrrrrR | (ky2, dy2)
rrrR + Grr == GrrrrrR | (ky2, dy2)
rrrR + Grrr == GrrrrrrR | (ky2, dy2)
rrrR + Grrrr == GrrrrrrrR | (ky2, dy2)
rrrR + Grrrrr == GrrrrrrrrR | (ky2, dy2)
rrrrR + Gr == GrrrrrR | (ky2, dy2)
rrrrR + Grr == GrrrrrrR | (ky2, dy2)
rrrrR + Grrr == GrrrrrrrR | (ky2, dy2)
rrrrR + Grrrr == GrrrrrrrrR | (ky2, dy2)
rrrrR + Grrrrr == GrrrrrrrrrR | (ky2, dy2)
GR + R == GRR | (ky3, dy3)
GR + rR == GrRR | (ky3, dy3)
GR + rrR == GrrRR | (ky3, dy3)
GR + rrrR == GrrrRR | (ky3, dy3)
GR + rrrrR == GrrrrRR | (ky3, dy3)
GrR + R == GrRR | (ky3, dy3)
GrR + rR == GrrRR | (ky3, dy3)
GrR + rrR == GrrrRR | (ky3, dy3)
GrR + rrrR == GrrrrRR | (ky3, dy3)
GrR + rrrrR == GrrrrrRR | (ky3, dy3)
GrrR + R == GrrRR | (ky3, dy3)
GrrR + rR == GrrrRR | (ky3, dy3)
GrrR + rrR == GrrrrRR | (ky3, dy3)
GrrR + rrrR == GrrrrrRR | (ky3, dy3)
GrrR + rrrrR == GrrrrrrRR | (ky3, dy3)
GrrrR + R == GrrrRR | (ky3, dy3)
GrrrR + rR == GrrrrRR | (ky3, dy3)
GrrrR + rrR == GrrrrrRR | (ky3, dy3)
GrrrR + rrrR == GrrrrrrRR | (ky3, dy3)
GrrrR + rrrrR == GrrrrrrrRR | (ky3, dy3)
GrrrrR + R == GrrrrRR | (ky3, dy3)
GrrrrR + rR == GrrrrrRR | (ky3, dy3)
GrrrrR + rrR == GrrrrrrRR | (ky3, dy3)
GrrrrR + rrrR == GrrrrrrrRR | (ky3, dy3)
GrrrrR + rrrrR == GrrrrrrrrRR | (ky3, dy3)
Grr == GrR | (ka1*L, da1)
Grrr == GrrR | (ka1*L, da1)
Grrrr == GrrrR | (ka1*L, da1)
Grrrrr == GrrrrR | (ka1*L, da1)
Grrrrrr == GrrrrrR | (ka1*L, da1)
Grrrrrrr == GrrrrrrR | (ka1*L, da1)
Grrrrrrrr == GrrrrrrrR | (ka1*L, da1)
Grrrrrrrrr == GrrrrrrrrR | (ka1*L, da1)
Grrrrrrrrrr == GrrrrrrrrrR | (ka1*L, da1)
GrR == GRR | (ka2*L, da2)
GrrR == GrRR | (ka2*L, da2)
GrrrR == GrrRR | (ka2*L, da2)
GrrrrR == GrrrRR | (ka2*L, da2)
GrrrrrR == GrrrrRR | (ka2*L, da2)
GrrrrrrR == GrrrrrRR | (ka2*L, da2)
GrrrrrrrR == GrrrrrrRR | (ka2*L, da2)
GrrrrrrrrR == GrrrrrrrRR | (ka2*L, da2)
GrrrrrrrrrR == GrrrrrrrrRR | (ka2*L, da2)
m = get_model()
show(m)
r > R | 1.0
R > r | 1.0
R > GR | 1.0
GR > R | 1.0
r > Gr | 1.0
Gr > r | 1.0
Gr > GR | 1.0
GR > Gr | 1.0
r + r > rr | 0.00020092425155716296
rr > r + r | 1.0
r + rr > rrr | 0.00020092425155716296
rrr > r + rr | 1.0
r + rrr > rrrr | 0.00020092425155716296
rrrr > r + rrr | 1.0
r + rrrr > rrrrr | 0.00020092425155716296
rrrrr > r + rrrr | 1.0
r + rrrrr > rrrrrr | 0.00020092425155716296
rrrrrr > r + rrrrr | 1.0
rr + r > rrr | 0.00020092425155716296
rrr > rr + r | 1.0
rr + rr > rrrr | 0.00020092425155716296
rrrr > rr + rr | 1.0
rr + rrr > rrrrr | 0.00020092425155716296
rrrrr > rr + rrr | 1.0
rr + rrrr > rrrrrr | 0.00020092425155716296
rrrrrr > rr + rrrr | 1.0
rr + rrrrr > rrrrrrr | 0.00020092425155716296
rrrrrrr > rr + rrrrr | 1.0
rrr + r > rrrr | 0.00020092425155716296
rrrr > rrr + r | 1.0
rrr + rr > rrrrr | 0.00020092425155716296
rrrrr > rrr + rr | 1.0
rrr + rrr > rrrrrr | 0.00020092425155716296
rrrrrr > rrr + rrr | 1.0
rrr + rrrr > rrrrrrr | 0.00020092425155716296
rrrrrrr > rrr + rrrr | 1.0
rrr + rrrrr > rrrrrrrr | 0.00020092425155716296
rrrrrrrr > rrr + rrrrr | 1.0
rrrr + r > rrrrr | 0.00020092425155716296
rrrrr > rrrr + r | 1.0
rrrr + rr > rrrrrr | 0.00020092425155716296
rrrrrr > rrrr + rr | 1.0
rrrr + rrr > rrrrrrr | 0.00020092425155716296
rrrrrrr > rrrr + rrr | 1.0
rrrr + rrrr > rrrrrrrr | 0.00020092425155716296
rrrrrrrr > rrrr + rrrr | 1.0
rrrr + rrrrr > rrrrrrrrr | 0.00020092425155716296
rrrrrrrrr > rrrr + rrrrr | 1.0
rrrrr + r > rrrrrr | 0.00020092425155716296
rrrrrr > rrrrr + r | 1.0
rrrrr + rr > rrrrrrr | 0.00020092425155716296
rrrrrrr > rrrrr + rr | 1.0
rrrrr + rrr > rrrrrrrr | 0.00020092425155716296
rrrrrrrr > rrrrr + rrr | 1.0
rrrrr + rrrr > rrrrrrrrr | 0.00020092425155716296
rrrrrrrrr > rrrrr + rrrr | 1.0
rrrrr + rrrrr > rrrrrrrrrr | 0.00020092425155716296
rrrrrrrrrr > rrrrr + rrrrr | 1.0
R + r > rR | 2.0092425155716294e-06
rR > R + r | 1.0
R + rr > rrR | 2.0092425155716294e-06
rrR > R + rr | 1.0
R + rrr > rrrR | 2.0092425155716294e-06
rrrR > R + rrr | 1.0
R + rrrr > rrrrR | 2.0092425155716294e-06
rrrrR > R + rrrr | 1.0
R + rrrrr > rrrrrR | 2.0092425155716294e-06
rrrrrR > R + rrrrr | 1.0
rR + r > rrR | 2.0092425155716294e-06
rrR > rR + r | 1.0
rR + rr > rrrR | 2.0092425155716294e-06
rrrR > rR + rr | 1.0
rR + rrr > rrrrR | 2.0092425155716294e-06
rrrrR > rR + rrr | 1.0
rR + rrrr > rrrrrR | 2.0092425155716294e-06
rrrrrR > rR + rrrr | 1.0
rR + rrrrr > rrrrrrR | 2.0092425155716294e-06
rrrrrrR > rR + rrrrr | 1.0
rrR + r > rrrR | 2.0092425155716294e-06
rrrR > rrR + r | 1.0
rrR + rr > rrrrR | 2.0092425155716294e-06
rrrrR > rrR + rr | 1.0
rrR + rrr > rrrrrR | 2.0092425155716294e-06
rrrrrR > rrR + rrr | 1.0
rrR + rrrr > rrrrrrR | 2.0092425155716294e-06
rrrrrrR > rrR + rrrr | 1.0
rrR + rrrrr > rrrrrrrR | 2.0092425155716294e-06
rrrrrrrR > rrR + rrrrr | 1.0
rrrR + r > rrrrR | 2.0092425155716294e-06
rrrrR > rrrR + r | 1.0
rrrR + rr > rrrrrR | 2.0092425155716294e-06
rrrrrR > rrrR + rr | 1.0
rrrR + rrr > rrrrrrR | 2.0092425155716294e-06
rrrrrrR > rrrR + rrr | 1.0
rrrR + rrrr > rrrrrrrR | 2.0092425155716294e-06
rrrrrrrR > rrrR + rrrr | 1.0
rrrR + rrrrr > rrrrrrrrR | 2.0092425155716294e-06
rrrrrrrrR > rrrR + rrrrr | 1.0
rrrrR + r > rrrrrR | 2.0092425155716294e-06
rrrrrR > rrrrR + r | 1.0
rrrrR + rr > rrrrrrR | 2.0092425155716294e-06
rrrrrrR > rrrrR + rr | 1.0
rrrrR + rrr > rrrrrrrR | 2.0092425155716294e-06
rrrrrrrR > rrrrR + rrr | 1.0
rrrrR + rrrr > rrrrrrrrR | 2.0092425155716294e-06
rrrrrrrrR > rrrrR + rrrr | 1.0
rrrrR + rrrrr > rrrrrrrrrR | 2.0092425155716294e-06
rrrrrrrrrR > rrrrR + rrrrr | 1.0
R + R > RR | 2.0092425155716296e-08
RR > R + R | 1.0
R + rR > rRR | 2.0092425155716296e-08
rRR > R + rR | 1.0
R + rrR > rrRR | 2.0092425155716296e-08
rrRR > R + rrR | 1.0
R + rrrR > rrrRR | 2.0092425155716296e-08
rrrRR > R + rrrR | 1.0
R + rrrrR > rrrrRR | 2.0092425155716296e-08
rrrrRR > R + rrrrR | 1.0
rR + R > rRR | 2.0092425155716296e-08
rRR > rR + R | 1.0
rR + rR > rrRR | 2.0092425155716296e-08
rrRR > rR + rR | 1.0
rR + rrR > rrrRR | 2.0092425155716296e-08
rrrRR > rR + rrR | 1.0
rR + rrrR > rrrrRR | 2.0092425155716296e-08
rrrrRR > rR + rrrR | 1.0
rR + rrrrR > rrrrrRR | 2.0092425155716296e-08
rrrrrRR > rR + rrrrR | 1.0
rrR + R > rrRR | 2.0092425155716296e-08
rrRR > rrR + R | 1.0
rrR + rR > rrrRR | 2.0092425155716296e-08
rrrRR > rrR + rR | 1.0
rrR + rrR > rrrrRR | 2.0092425155716296e-08
rrrrRR > rrR + rrR | 1.0
rrR + rrrR > rrrrrRR | 2.0092425155716296e-08
rrrrrRR > rrR + rrrR | 1.0
rrR + rrrrR > rrrrrrRR | 2.0092425155716296e-08
rrrrrrRR > rrR + rrrrR | 1.0
rrrR + R > rrrRR | 2.0092425155716296e-08
rrrRR > rrrR + R | 1.0
rrrR + rR > rrrrRR | 2.0092425155716296e-08
rrrrRR > rrrR + rR | 1.0
rrrR + rrR > rrrrrRR | 2.0092425155716296e-08
rrrrrRR > rrrR + rrR | 1.0
rrrR + rrrR > rrrrrrRR | 2.0092425155716296e-08
rrrrrrRR > rrrR + rrrR | 1.0
rrrR + rrrrR > rrrrrrrRR | 2.0092425155716296e-08
rrrrrrrRR > rrrR + rrrrR | 1.0
rrrrR + R > rrrrRR | 2.0092425155716296e-08
rrrrRR > rrrrR + R | 1.0
rrrrR + rR > rrrrrRR | 2.0092425155716296e-08
rrrrrRR > rrrrR + rR | 1.0
rrrrR + rrR > rrrrrrRR | 2.0092425155716296e-08
rrrrrrRR > rrrrR + rrR | 1.0
rrrrR + rrrR > rrrrrrrRR | 2.0092425155716296e-08
rrrrrrrRR > rrrrR + rrrR | 1.0
rrrrR + rrrrR > rrrrrrrrRR | 2.0092425155716296e-08
rrrrrrrrRR > rrrrR + rrrrR | 1.0
rr > rR | 0.01
rR > rr | 1.0
rrr > rrR | 0.01
rrR > rrr | 1.0
rrrr > rrrR | 0.01
rrrR > rrrr | 1.0
rrrrr > rrrrR | 0.01
rrrrR > rrrrr | 1.0
rrrrrr > rrrrrR | 0.01
rrrrrR > rrrrrr | 1.0
rrrrrrr > rrrrrrR | 0.01
rrrrrrR > rrrrrrr | 1.0
rrrrrrrr > rrrrrrrR | 0.01
rrrrrrrR > rrrrrrrr | 1.0
rrrrrrrrr > rrrrrrrrR | 0.01
rrrrrrrrR > rrrrrrrrr | 1.0
rrrrrrrrrr > rrrrrrrrrR | 0.01
rrrrrrrrrR > rrrrrrrrrr | 1.0
rR > RR | 0.01
RR > rR | 1.0
rrR > rRR | 0.01
rRR > rrR | 1.0
rrrR > rrRR | 0.01
rrRR > rrrR | 1.0
rrrrR > rrrRR | 0.01
rrrRR > rrrrR | 1.0
rrrrrR > rrrrRR | 0.01
rrrrRR > rrrrrR | 1.0
rrrrrrR > rrrrrRR | 0.01
rrrrrRR > rrrrrrR | 1.0
rrrrrrrR > rrrrrrRR | 0.01
rrrrrrRR > rrrrrrrR | 1.0
rrrrrrrrR > rrrrrrrRR | 0.01
rrrrrrrRR > rrrrrrrrR | 1.0
rrrrrrrrrR > rrrrrrrrRR | 0.01
rrrrrrrrRR > rrrrrrrrrR | 1.0
rr > Grr | 0.01
Grr > rr | 1.0
rrr > Grrr | 0.01
Grrr > rrr | 1.0
rrrr > Grrrr | 0.01
Grrrr > rrrr | 1.0
rrrrr > Grrrrr | 0.01
Grrrrr > rrrrr | 1.0
rrrrrr > Grrrrrr | 0.01
Grrrrrr > rrrrrr | 1.0
rrrrrrr > Grrrrrrr | 0.01
Grrrrrrr > rrrrrrr | 1.0
rrrrrrrr > Grrrrrrrr | 0.01
Grrrrrrrr > rrrrrrrr | 1.0
rrrrrrrrr > Grrrrrrrrr | 0.01
Grrrrrrrrr > rrrrrrrrr | 1.0
rrrrrrrrrr > Grrrrrrrrrr | 0.01
Grrrrrrrrrr > rrrrrrrrrr | 1.0
rR > GrR | 0.01
GrR > rR | 1.0
rrR > GrrR | 0.01
GrrR > rrR | 1.0
rrrR > GrrrR | 0.01
GrrrR > rrrR | 1.0
rrrrR > GrrrrR | 0.01
GrrrrR > rrrrR | 1.0
rrrrrR > GrrrrrR | 0.01
GrrrrrR > rrrrrR | 1.0
rrrrrrR > GrrrrrrR | 0.01
GrrrrrrR > rrrrrrR | 1.0
rrrrrrrR > GrrrrrrrR | 0.01
GrrrrrrrR > rrrrrrrR | 1.0
rrrrrrrrR > GrrrrrrrrR | 0.01
GrrrrrrrrR > rrrrrrrrR | 1.0
rrrrrrrrrR > GrrrrrrrrrR | 0.01
GrrrrrrrrrR > rrrrrrrrrR | 1.0
RR > GRR | 0.01
GRR > RR | 1.0
rRR > GrRR | 0.01
GrRR > rRR | 1.0
rrRR > GrrRR | 0.01
GrrRR > rrRR | 1.0
rrrRR > GrrrRR | 0.01
GrrrRR > rrrRR | 1.0
rrrrRR > GrrrrRR | 0.01
GrrrrRR > rrrrRR | 1.0
rrrrrRR > GrrrrrRR | 0.01
GrrrrrRR > rrrrrRR | 1.0
rrrrrrRR > GrrrrrrRR | 0.01
GrrrrrrRR > rrrrrrRR | 1.0
rrrrrrrRR > GrrrrrrrRR | 0.01
GrrrrrrrRR > rrrrrrrRR | 1.0
rrrrrrrrRR > GrrrrrrrrRR | 0.01
GrrrrrrrrRR > rrrrrrrrRR | 1.0
Gr + r > Grr | 0.00020092425155716296
Grr > Gr + r | 1.0
Gr + rr > Grrr | 0.00020092425155716296
Grrr > Gr + rr | 1.0
Gr + rrr > Grrrr | 0.00020092425155716296
Grrrr > Gr + rrr | 1.0
Gr + rrrr > Grrrrr | 0.00020092425155716296
Grrrrr > Gr + rrrr | 1.0
Gr + rrrrr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Gr + rrrrr | 1.0
Grr + r > Grrr | 0.00020092425155716296
Grrr > Grr + r | 1.0
Grr + rr > Grrrr | 0.00020092425155716296
Grrrr > Grr + rr | 1.0
Grr + rrr > Grrrrr | 0.00020092425155716296
Grrrrr > Grr + rrr | 1.0
Grr + rrrr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grr + rrrr | 1.0
Grr + rrrrr > Grrrrrrr | 0.00020092425155716296
Grrrrrrr > Grr + rrrrr | 1.0
Grrr + r > Grrrr | 0.00020092425155716296
Grrrr > Grrr + r | 1.0
Grrr + rr > Grrrrr | 0.00020092425155716296
Grrrrr > Grrr + rr | 1.0
Grrr + rrr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grrr + rrr | 1.0
Grrr + rrrr > Grrrrrrr | 0.00020092425155716296
Grrrrrrr > Grrr + rrrr | 1.0
Grrr + rrrrr > Grrrrrrrr | 0.00020092425155716296
Grrrrrrrr > Grrr + rrrrr | 1.0
Grrrr + r > Grrrrr | 0.00020092425155716296
Grrrrr > Grrrr + r | 1.0
Grrrr + rr > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grrrr + rr | 1.0
Grrrr + rrr > Grrrrrrr | 0.00020092425155716296
Grrrrrrr > Grrrr + rrr | 1.0
Grrrr + rrrr > Grrrrrrrr | 0.00020092425155716296
Grrrrrrrr > Grrrr + rrrr | 1.0
Grrrr + rrrrr > Grrrrrrrrr | 0.00020092425155716296
Grrrrrrrrr > Grrrr + rrrrr | 1.0
Grrrrr + r > Grrrrrr | 0.00020092425155716296
Grrrrrr > Grrrrr + r | 1.0
Grrrrr + rr > Grrrrrrr | 0.00020092425155716296
Grrrrrrr > Grrrrr + rr | 1.0
Grrrrr + rrr > Grrrrrrrr | 0.00020092425155716296
Grrrrrrrr > Grrrrr + rrr | 1.0
Grrrrr + rrrr > Grrrrrrrrr | 0.00020092425155716296
Grrrrrrrrr > Grrrrr + rrrr | 1.0
Grrrrr + rrrrr > Grrrrrrrrrr | 0.00020092425155716296
Grrrrrrrrrr > Grrrrr + rrrrr | 1.0
GR + r > GrR | 2.0092425155716294e-06
GrR > GR + r | 1.0
GR + rr > GrrR | 2.0092425155716294e-06
GrrR > GR + rr | 1.0
GR + rrr > GrrrR | 2.0092425155716294e-06
GrrrR > GR + rrr | 1.0
GR + rrrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GR + rrrr | 1.0
GR + rrrrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GR + rrrrr | 1.0
GrR + r > GrrR | 2.0092425155716294e-06
GrrR > GrR + r | 1.0
GrR + rr > GrrrR | 2.0092425155716294e-06
GrrrR > GrR + rr | 1.0
GrR + rrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrR + rrr | 1.0
GrR + rrrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrR + rrrr | 1.0
GrR + rrrrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > GrR + rrrrr | 1.0
GrrR + r > GrrrR | 2.0092425155716294e-06
GrrrR > GrrR + r | 1.0
GrrR + rr > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrrR + rr | 1.0
GrrR + rrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrrR + rrr | 1.0
GrrR + rrrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > GrrR + rrrr | 1.0
GrrR + rrrrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > GrrR + rrrrr | 1.0
GrrrR + r > GrrrrR | 2.0092425155716294e-06
GrrrrR > GrrrR + r | 1.0
GrrrR + rr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrrrR + rr | 1.0
GrrrR + rrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > GrrrR + rrr | 1.0
GrrrR + rrrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > GrrrR + rrrr | 1.0
GrrrR + rrrrr > GrrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrrR > GrrrR + rrrrr | 1.0
GrrrrR + r > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > GrrrrR + r | 1.0
GrrrrR + rr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > GrrrrR + rr | 1.0
GrrrrR + rrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > GrrrrR + rrr | 1.0
GrrrrR + rrrr > GrrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrrR > GrrrrR + rrrr | 1.0
GrrrrR + rrrrr > GrrrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrrrR > GrrrrR + rrrrr | 1.0
R + Gr > GrR | 2.0092425155716294e-06
GrR > R + Gr | 1.0
R + Grr > GrrR | 2.0092425155716294e-06
GrrR > R + Grr | 1.0
R + Grrr > GrrrR | 2.0092425155716294e-06
GrrrR > R + Grrr | 1.0
R + Grrrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > R + Grrrr | 1.0
R + Grrrrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > R + Grrrrr | 1.0
rR + Gr > GrrR | 2.0092425155716294e-06
GrrR > rR + Gr | 1.0
rR + Grr > GrrrR | 2.0092425155716294e-06
GrrrR > rR + Grr | 1.0
rR + Grrr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rR + Grrr | 1.0
rR + Grrrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rR + Grrrr | 1.0
rR + Grrrrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > rR + Grrrrr | 1.0
rrR + Gr > GrrrR | 2.0092425155716294e-06
GrrrR > rrR + Gr | 1.0
rrR + Grr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rrR + Grr | 1.0
rrR + Grrr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rrR + Grrr | 1.0
rrR + Grrrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > rrR + Grrrr | 1.0
rrR + Grrrrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > rrR + Grrrrr | 1.0
rrrR + Gr > GrrrrR | 2.0092425155716294e-06
GrrrrR > rrrR + Gr | 1.0
rrrR + Grr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rrrR + Grr | 1.0
rrrR + Grrr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > rrrR + Grrr | 1.0
rrrR + Grrrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > rrrR + Grrrr | 1.0
rrrR + Grrrrr > GrrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrrR > rrrR + Grrrrr | 1.0
rrrrR + Gr > GrrrrrR | 2.0092425155716294e-06
GrrrrrR > rrrrR + Gr | 1.0
rrrrR + Grr > GrrrrrrR | 2.0092425155716294e-06
GrrrrrrR > rrrrR + Grr | 1.0
rrrrR + Grrr > GrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrR > rrrrR + Grrr | 1.0
rrrrR + Grrrr > GrrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrrR > rrrrR + Grrrr | 1.0
rrrrR + Grrrrr > GrrrrrrrrrR | 2.0092425155716294e-06
GrrrrrrrrrR > rrrrR + Grrrrr | 1.0
GR + R > GRR | 2.0092425155716296e-08
GRR > GR + R | 1.0
GR + rR > GrRR | 2.0092425155716296e-08
GrRR > GR + rR | 1.0
GR + rrR > GrrRR | 2.0092425155716296e-08
GrrRR > GR + rrR | 1.0
GR + rrrR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GR + rrrR | 1.0
GR + rrrrR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GR + rrrrR | 1.0
GrR + R > GrRR | 2.0092425155716296e-08
GrRR > GrR + R | 1.0
GrR + rR > GrrRR | 2.0092425155716296e-08
GrrRR > GrR + rR | 1.0
GrR + rrR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrR + rrR | 1.0
GrR + rrrR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrR + rrrR | 1.0
GrR + rrrrR > GrrrrrRR | 2.0092425155716296e-08
GrrrrrRR > GrR + rrrrR | 1.0
GrrR + R > GrrRR | 2.0092425155716296e-08
GrrRR > GrrR + R | 1.0
GrrR + rR > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrrR + rR | 1.0
GrrR + rrR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrrR + rrR | 1.0
GrrR + rrrR > GrrrrrRR | 2.0092425155716296e-08
GrrrrrRR > GrrR + rrrR | 1.0
GrrR + rrrrR > GrrrrrrRR | 2.0092425155716296e-08
GrrrrrrRR > GrrR + rrrrR | 1.0
GrrrR + R > GrrrRR | 2.0092425155716296e-08
GrrrRR > GrrrR + R | 1.0
GrrrR + rR > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrrrR + rR | 1.0
GrrrR + rrR > GrrrrrRR | 2.0092425155716296e-08
GrrrrrRR > GrrrR + rrR | 1.0
GrrrR + rrrR > GrrrrrrRR | 2.0092425155716296e-08
GrrrrrrRR > GrrrR + rrrR | 1.0
GrrrR + rrrrR > GrrrrrrrRR | 2.0092425155716296e-08
GrrrrrrrRR > GrrrR + rrrrR | 1.0
GrrrrR + R > GrrrrRR | 2.0092425155716296e-08
GrrrrRR > GrrrrR + R | 1.0
GrrrrR + rR > GrrrrrRR | 2.0092425155716296e-08
GrrrrrRR > GrrrrR + rR | 1.0
GrrrrR + rrR > GrrrrrrRR | 2.0092425155716296e-08
GrrrrrrRR > GrrrrR + rrR | 1.0
GrrrrR + rrrR > GrrrrrrrRR | 2.0092425155716296e-08
GrrrrrrrRR > GrrrrR + rrrR | 1.0
GrrrrR + rrrrR > GrrrrrrrrRR | 2.0092425155716296e-08
GrrrrrrrrRR > GrrrrR + rrrrR | 1.0
Grr > GrR | 0.01
GrR > Grr | 1.0
Grrr > GrrR | 0.01
GrrR > Grrr | 1.0
Grrrr > GrrrR | 0.01
GrrrR > Grrrr | 1.0
Grrrrr > GrrrrR | 0.01
GrrrrR > Grrrrr | 1.0
Grrrrrr > GrrrrrR | 0.01
GrrrrrR > Grrrrrr | 1.0
Grrrrrrr > GrrrrrrR | 0.01
GrrrrrrR > Grrrrrrr | 1.0
Grrrrrrrr > GrrrrrrrR | 0.01
GrrrrrrrR > Grrrrrrrr | 1.0
Grrrrrrrrr > GrrrrrrrrR | 0.01
GrrrrrrrrR > Grrrrrrrrr | 1.0
Grrrrrrrrrr > GrrrrrrrrrR | 0.01
GrrrrrrrrrR > Grrrrrrrrrr | 1.0
GrR > GRR | 0.01
GRR > GrR | 1.0
GrrR > GrRR | 0.01
GrRR > GrrR | 1.0
GrrrR > GrrRR | 0.01
GrrRR > GrrrR | 1.0
GrrrrR > GrrrRR | 0.01
GrrrRR > GrrrrR | 1.0
GrrrrrR > GrrrrRR | 0.01
GrrrrRR > GrrrrrR | 1.0
GrrrrrrR > GrrrrrRR | 0.01
GrrrrrRR > GrrrrrrR | 1.0
GrrrrrrrR > GrrrrrrRR | 0.01
GrrrrrrRR > GrrrrrrrR | 1.0
GrrrrrrrrR > GrrrrrrrRR | 0.01
GrrrrrrrRR > GrrrrrrrrR | 1.0
GrrrrrrrrrR > GrrrrrrrrRR | 0.01
GrrrrrrrrRR > GrrrrrrrrrR | 1.0
[26]:
obs0 = numpy.zeros(shape=(len(mols)))
obs0[0] = par.get_r0()
run_N5(m, mols, obs0)
Initial condition
r : 49770
rr : 0
rrr : 0
rrrr : 0
rrrrr : 0
rrrrrr : 0
rrrrrrr : 0
rrrrrrrr : 0
rrrrrrrr : 0
rrrrrrrrrr : 0
R : 0
rR : 0
rrR : 0
rrrR : 0
rrrrR : 0
rrrrrR : 0
rrrrrrR : 0
rrrrrrrR : 0
rrrrrrrR : 0
rrrrrrrrrR : 0
RR : 0
rRR : 0
rrRR : 0
rrrRR : 0
rrrrRR : 0
rrrrrRR : 0
rrrrrrRR : 0
rrrrrrRR : 0
rrrrrrrrRR : 0
Gr : 0
Grr : 0
Grrr : 0
Grrrr : 0
Grrrrr : 0
Grrrrrr : 0
Grrrrrrr : 0
Grrrrrrrr : 0
Grrrrrrrr : 0
Grrrrrrrrrr : 0
GR : 0
GrR : 0
GrrR : 0
GrrrR : 0
GrrrrR : 0
GrrrrrR : 0
GrrrrrrR : 0
GrrrrrrrR : 0
GrrrrrrrR : 0
GrrrrrrrrrR : 0
GRR : 0
GrRR : 0
GrrRR : 0
GrrrRR : 0
GrrrrRR : 0
GrrrrrRR : 0
GrrrrrrRR : 0
GrrrrrrRR : 0
GrrrrrrrrRR : 0